A masonary column of density ρ has height h top cross sectional area A1 and bottom cross sectional area A2. Top cross sectional of the column is uniformly loaded with load F. If stress at any cross section of the column is same and ρghA1=2F, the integer closest to A2A1 is
NA
Topper's Solved these Questions
Similar Questions
A force F is applied on a block of mass 5kg as shown in figure. Co-efficient of friction between the wall and clock is √32.(g=10m/s2)
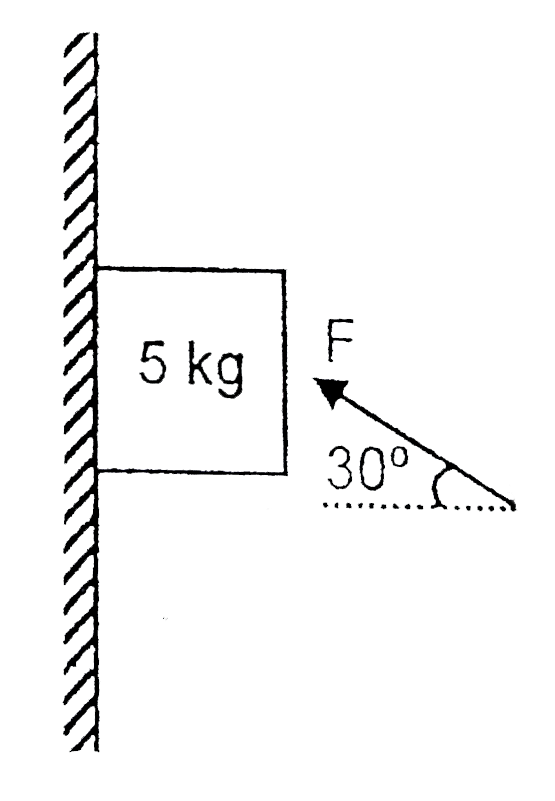
Select correct option(s)
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionA horizontal tube has different cross sections at points A and B. The areas of cross section are a1 and a2 respectively, and pressures at these points are p1=ρgh1 and p2=ρgh2 where ρ is the density of liquid flowing in the tube and h1 and h2 are heights of liquid columns in vertical tubes connected at A and B. If h1−h2=h, then the flow rate of the liquid in the horizontal tube is
View SolutionA portion of a tube is shown in the figure. Fluid is flowing from cross-section area A1 to A2. The two cross-sections are at distance 'l' from each other. The velocity of the fluid at section A2 is √gl2. If the pressures at A1 & A2 are same, then the angle made by the tube with the horizontal will be:
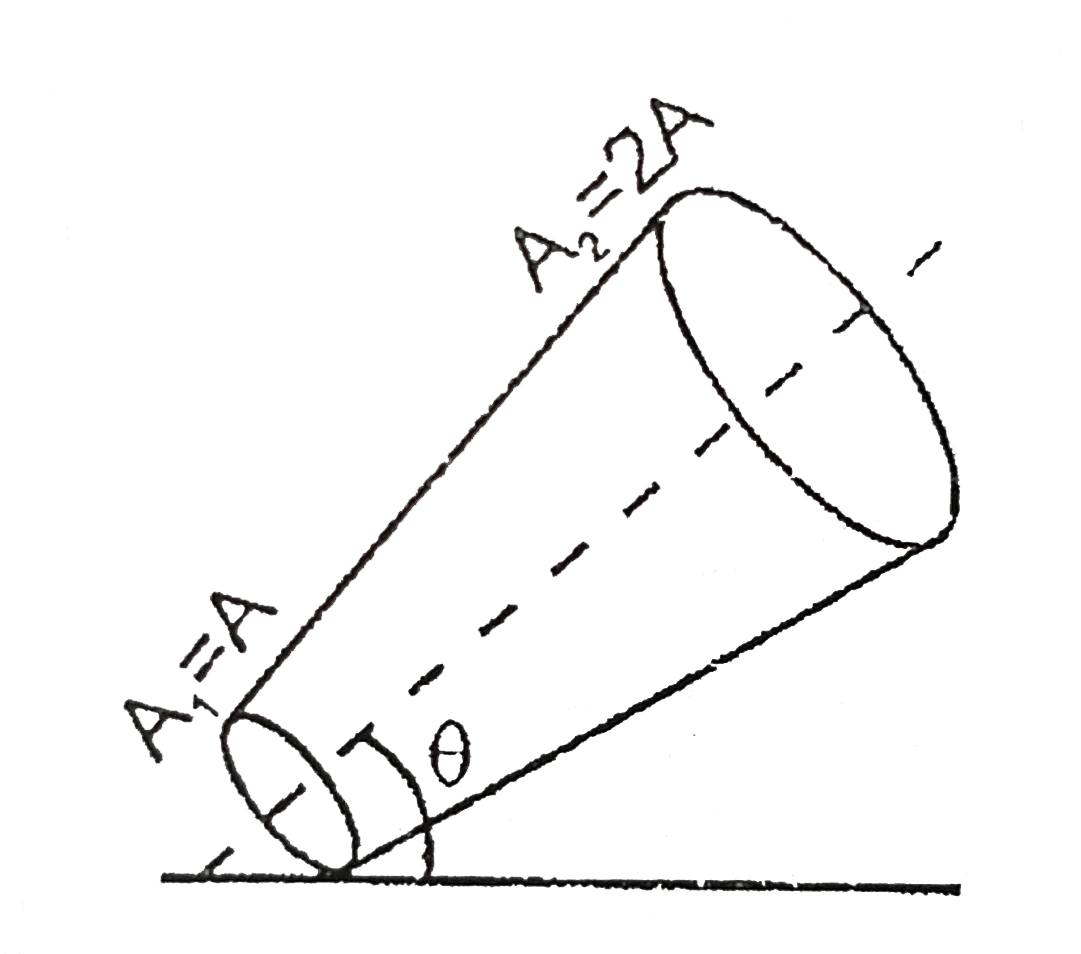
View SolutionA masonary column of density rho has height h top cross sectional area A_(1) and bottom cross sectional area A_(2) . Top cross sectional of the column is uniformly loaded with load F . If stress at any cross section of the column is same and rhoghA_(1)=2F , the integer closest to (A_(2))/(A_(1)) is
View SolutionThe velocity of an electron at point A_(1) is V_(0) where cross sectional area is A. The velocity of electron at the end of contraction at point B, where cross sectional area is 2A, is V_(1) . Find the correct option:
View SolutionFrom a horizontal tube with area of cross-section A_(1) and A_(2) as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)

View SolutionA liquid flows through a pipe of non-uniform cross-section. If A_(1) and A_(2) are the cross-sectional areas of the pipe at two points, the ratio of velocities of the liquid at these points will be
View Solutiona1 প্রস্থছেদের ক্ষেত্রফল সম্পন্ন চোঙাকৃতি একটি জলাধার h উচ্চতা পর্যন্ত জলপুর্ণ। জলাধারের তলদেশেa2ক্ষেত্রফলের একটি ছিদ্র আছে।প্রদত্ত যে,a1=3a2।
জলাধারের জলতল হ্রাসের প্রাথমিক বেগ হল
View Solutiona_(1) A reservoir filled with cross-sectional area is waterlogged to a height of h. At the bottom of the reservoir a_(2) There is a hole in the area. a_(1)=3a_(2) The initial velocity of water coming out through the hole is
View Solutiona1 প্রস্থছেদের ক্ষেত্রফল সম্পন্ন চোঙাকৃতি একটি জলাধার h উচ্চতা পর্যন্ত জলপুর্ণ। জলাধারের তলদেশেa2 ক্ষেত্রফলের একটি ছিদ্র আছে।প্রদত্ত যে,a1=3a2।
জলাধারটি সম্পূর্ণ খালি হতে যে সময় নেবে তা হল
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)

View SolutionA horizontal tube has different cross sections at points A and B . The areas of cross section are a_(1) and a_(2) respectively, and pressures at these points are p_(1)=rhogh_(1) and p_(2)=rhogh_(2) where rho is the density of liquid flowing in the tube and h_(1) and h_(2) are heights of liquid columns in vertical tubes connected at A and B . If h_(1)-h_(2)=h , then the flow rate of the liquid in the horizontal tube is
View SolutionThe velocity of an electron at point A1 is V0 where cross sectional area is A. The velocity of electron at the end of contraction at point B, where cross sectional area is 2A, is V1. Find the correct option:
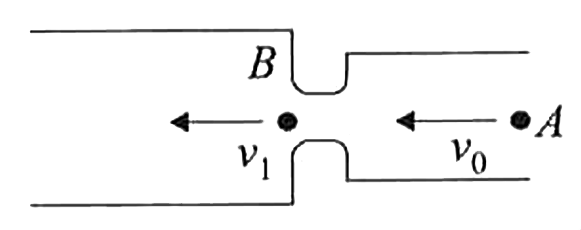
View SolutionA portion of a tube is shown in the figure. Fluid is flowing from cross-section area A_(1) to A_(2) . The two cross-sections are at distance 'l' from each other. The velocity of the fluid at section A_(2) is sqrt((gl)/(2)) . If the pressures at A_(1) & A_(2) are same, then the angle made by the tube with the horizontal will be:
View Solution

