A rod of length l and total charge 'q' which is uniformly distributed is rotating with angular velocity ω about an axis passing through the centre of rod and perpendicular to rod. Find the magnitude of magnetic dipole moment (in Amp. m2) of rod. If q=4C,ω=3rad/s and l=2m
NA
Topper's Solved these Questions
Similar Questions
A force F is applied on a block of mass 5kg as shown in figure. Co-efficient of friction between the wall and clock is √32.(g=10m/s2)
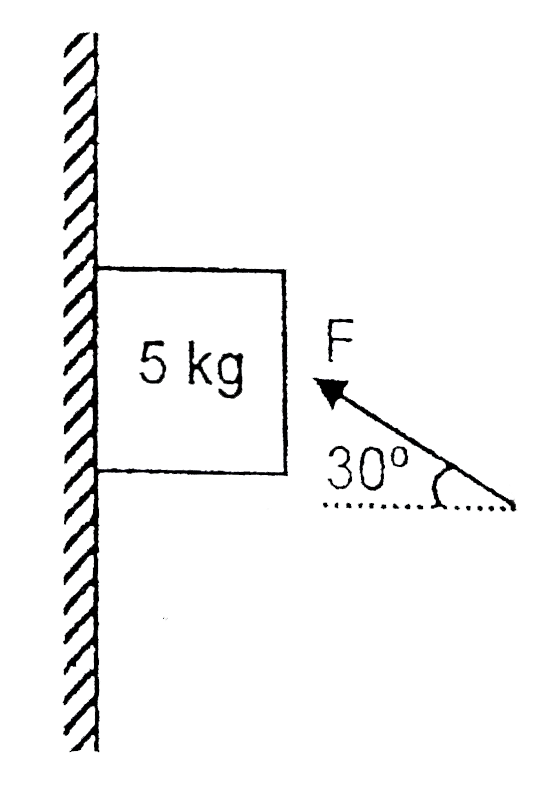
Select correct option(s)
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity omega about its end, compute its magnetic moment.
View SolutionA conical pendulum, a thin uniform rod of length l and mass m , rotates uniformly about a vertical axis with angular velocity omega (the upper end of the rod is hinged). Find the angle theta between the rod and the vertical.
View SolutionA rod of length l and total charge 'q' which is uniformly distributed is rotating with angular velocity ω about an axis passing through the centre of rod and perpendicular to rod. Find the magnitude of magnetic dipole moment (in Amp. m2) of rod. If q=4C,ω=3rad/s and l=2m
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA thin uniform rod of mass M and length L is rotating about a perpendicular axis passing through its centre with a constant angular velocity ω. Two objects each of mass M3 are attached gently to the two end of the rod. The rod will now rotate with an angular velocity of
View SolutionA rod of length L rotates about an axis passing through its centre and normal to its length with an angular velocity ω. If A is the cross section and D is the density of material of rod, its rotational K.E. is :
View SolutionA uniform rod of mass M and length L carrying a charge q uniformly distributed over its length is rotated with constant velocity w about its mid point perpendicular to the rod. Its magnetic moment is
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionAn insulating rod of length l and charge carries q distributed uniformly on it. The rod is pivoted at its one end and it rotated with angular velocity omega about a fix axis perpendicular to the rod and passing through the pivot. The magnetic moment of rhe system is
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity omega about its end, compute its magnetic moment.
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.

View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through ts centre. Find the ratio of the magnetic moment of the system and its angular momentum about the axis through the centre of the rod.
View Solution

