The speed (v) of a particle moving along a straight line, when it is at a distance (x) from a fixed point on the line, is given by v2=144−9x2. Select correct alternate.
the motion is uniformly acclerated along the straight line
the magnitude of the acceleration at a distance 3cm from the fixed point is 27cm/s
The motion is simple harmonic about the given fixed point.
the maximum displacement displacment from the fixed point is 4cm.
The correct Answer is:B, C
Step by step video solution for The speed (v) of a particle moving along a straight line, when it is at a distance (x) from a fixed point on the line, is given by v^(2)=144-9x^(2). Select correct alternate. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - IV
Explore 8 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - I
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 105 Videos
Similar Questions
A 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5m/s2 when the acceleration suddenly ceases at time t=0 and the car moves upward with constant speed (g=10m/s2)
What is the angular frequencyof the block after the acceleration ceases ?
View SolutionA simple pendulum has time period T1. The point of suspension is now moved upward according to the relation y=Kt2. (K=1ms−2) where y is the vertical displacement. The time period now becomes T2
The ratio of T21T22(Take g=10ms−2)
View SolutionTwo particles A and B are performing SHM along x and y-axis respectively with equal amplitude and frequency of 2cm and 1Hz respectively. Equilibrium positions of the particles A and B are at the coordinates [3cm,0] and (0,4cm) respectively. At t=0,B is at its equilibrium position and moving towards the origin, while A is nearest to the origin and moving away from the origin-
Equation of motion of particle B can be written as-
View SolutionWhen p−n junction diode is forward biased, then
View SolutionA force F is applied on a block of mass 5kg as shown in figure. Co-efficient of friction between the wall and clock is √32.(g=10m/s2)
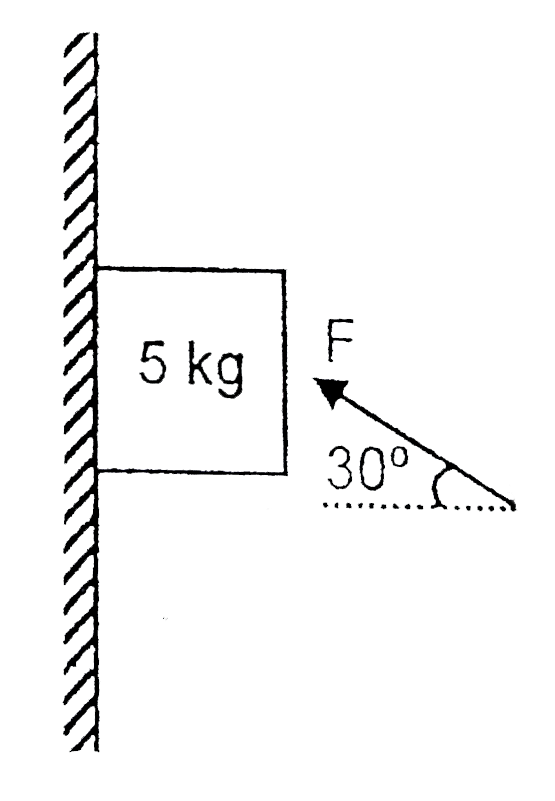
Select correct option(s)
View SolutionThe speed v of a particle moving along a straight line, when it is at a distance (x) from a fixed point of the line is given by v2=108−9x2 (all equation are in CGS units):
View SolutionSpeed v of a particle moving along a straight line, when it is a distance X from a fixed point on the line is given by V2=108−9X2 (all quantities in S.I. unit). Then
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v^(2)=144-9x^(2) . Select the correct alternatives
View SolutionThe speed (v) of particle moving along a straight line, when it is of a distance (x) from a fixed point on the line, is given by : v2=144−9x2
_S01_056_Q01.png)
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionIf the velocity v of a particle moving along a straight line and its distance s from a fixed point on the line are related by v2=a2+s2, then its acceleration equals
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2, where x is its distance from the origin. The acceleration of the particle is
View SolutionThe speed v of a particle moving along a straight line, when it is at a distance (x) from a fixed point on the line, is given by v2=144−9x2.
View SolutionThe speed v of a particle moving along a straight line, when it is at a distance (x) from a fixed point of the line is given by v^2 = 108 - 9x^2 (all quantities are in CGS units):
View SolutionThe speed v of particle moving along a straight line, when it is at a distance x from a fixed point on the line is given by v^2= 108 x - 9x^2 . Then magnitude of its acceleration when it is a distance 3 metre from the fixed point is
View SolutionThe speed v of a particle moving along a straight line. When it is at distance x from a fixed point on the line is v^(2)=144-9x^(2) . Select the correct alternatives
View Solution
