A simple pendulum has time period T1. The point of suspension is now moved upward according to the relation y=Kt2. (K=1ms−2) where y is the vertical
displacement. The time period now becomes T2
The ratio of T21T22(Take g=10ms−2)
56
65
1
45
The correct Answer is:B
T1=2π√lg=2π√l10
upward accelertion d2ydt2=2k=2×1=2m/s2
∴ Acceleration w.r.t. point of suspension =12m/s2
T2=2π√l12∴T1T2=√1210∴(T1T2)2=65
T1=2π√lg=2π√l10
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - II
Explore 17 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - IV
Explore 8 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 105 Videos
Similar Questions
If a simple harmonic motion is represented by d2xdt2+αx=0, its time period is
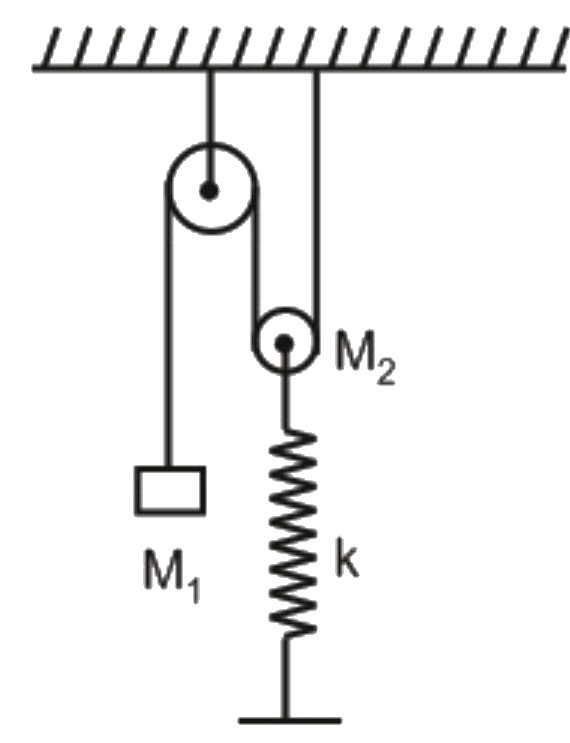
View SolutionA block of mass M1 is constrained to move along with a moveable pulley of mass M2 which is connected to a sprin of force constant k, as shown in the figure. If the mass of the fixed pulley is negligible and friction is absent everywhere, then the period of small oscillations of the system is
View SolutionA 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5m/s2 when the acceleration suddenly ceases at time t=0 and the car moves upward with constant speed (g=10m/s2)
What is the angular frequencyof the block after the acceleration ceases ?
View SolutionWhen p−n junction diode is forward biased, then
View SolutionA force F is applied on a block of mass 5kg as shown in figure. Co-efficient of friction between the wall and clock is √32.(g=10m/s2)
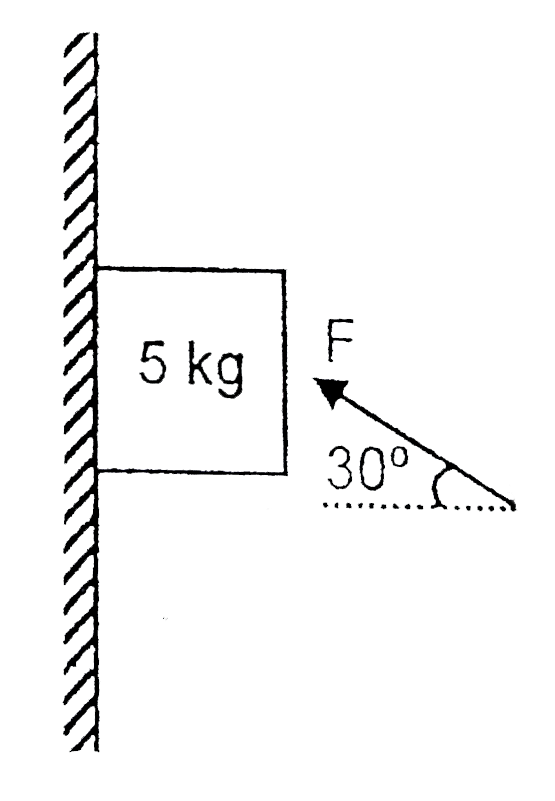
Select correct option(s)
View SolutionA simple pendulum has time period (T_1). The point of suspension is now moved upward according to the relation y = K t^2, (K = 1 m//s^2) where (y) is the vertical displacement. The time period now becomes (T_2). The ratio of (T_1^2)/(T_2^2) is (g = 10 m//s^2) .
View SolutionA simple pendulum has time period 2s. The point of suspension is now moved upward accoding to relation y=(6t−3.75t2)m where t is in second and y is the vertical displacement in upward direction. The new time period of simple pendulum will be
View SolutionA simple pendulum has time period T_(1) / The point of suspension is now moved upward according to the realtion y = kt^(2)(k = 1 m//s^(2)) where y is vertical displacement, the time period now becomes T_(2) . The ratio of ((T_(1))/(T_(2)))^(2) is : (g = 10 m//s^(2))
View Solutionएक सरल लोलक का आवर्तकाल T1 है जब इसके निलंबन-बिंदु को ऊर्ध्वाधर ऊपर की ओर y=kt2 के अनुशार चलाया जाता है , जहाँ y ऊर्ध्वाधर चली गई दूरी है तथा k = 1 मीटर/सेकण्ड2 है तब इसका आवर्तकाल हो T2 जाता है T21/T22 का मान है
( g=10 मीटर/सेकण्ड2)
View SolutionA simple pendulum has a time period of 3 s. If the point of suspension of the pendulum starts moving vertically upwards with a velocity =v=kt where k=4.4 m//s^(2) , the new time period will be (Take g=10 m//s^(2))
View SolutionA simple pendulum has time period T1. The point of suspension is now moved upwards according to the relation y=Kt2,(K=1m⋅s−2) where y is the vertical displacement. The time period now becomes T2. The ratio of T21/T22 is (g=10m⋅s−2)
View SolutionThe period of a displacement pendulum when the support point is fixed T_1 . The support point of the simple pendulum is being moved upwards. The relation of the upward movement y of the pendulum over time is: y=Kt^2 (K=1m* s^-2) . If the period of the pendulum changes T_2 Yes, then T_1^2/T_2^2 It will have value
View SolutionA simple pendulu has a time period T_(1) . The point of suspension of the pendulum is moved upword according to the relation y= (3)/(2)t^(2) , Where y is the vertical displacement . If the new time period is T_(2) , The ratio of (T_(1)^(2))/(T_(2)^(2)) is ( g=10m//s^(2))
View SolutionA simple pendulum has time period T_1 . The point of suspension is now moved upward according to the relation y = Kt^2(K = 1 m//s^2) where y is the vertical displacement as a function of time 't'. The time period now becomes T_2 . The ratio of (T_1^2)/(T_2^2) is 6/N where 'N' is equal to (g = 10m//s^2)
View SolutionA simple pendulum has time period (T_1). The point of suspension is now moved upward according to the relation y=Kt2,(K=1m/s2) where (y) is the vertical displacement. The time period now becomes (T_2). The ratio of T21T22 is (g=10m/s2).
View SolutionA simple pendulum has time period ' T_(1) '. The point of suspension is now moved upwards according to the relation y = kt^(2), (k = 1m//"sec"^(2)) where y is the vertical displacement. The time period now becomes ' T_(2) ' then find the ratio of (T_(1)^(2))/(T_(2)^(2)) (g= 10m//"sec")
View Solution
