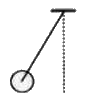
A metal rod of length 'L' and mass 'm' is pivoted at one end. A thin disk of mass 'M' and radius 'R' (< L) is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A) - The disc is not free to rotate about its centre and (case B) - the disc is free to rotate about its centre. The rod-disc system after being released from the same displaced position. Which of the following statement(s) is(are) true?
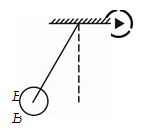
Restoring torque in case A = Restoring torque in caseB
Restoring torque in case A< Restoring torque in caseB
Restoring frequency case A> Angular frequency for caseB
Restoring frequency case A< Angular frequency for caseB
The correct Answer is:A, D
Tprque is same for both the cases.
T=2π√Imgd
IA>TB
ωA<ωB
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 3, PART - II
Explore 17 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - IV
Explore 8 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 105 Videos
Similar Questions
If a simple harmonic motion is represented by d2xdt2+αx=0, its time period is
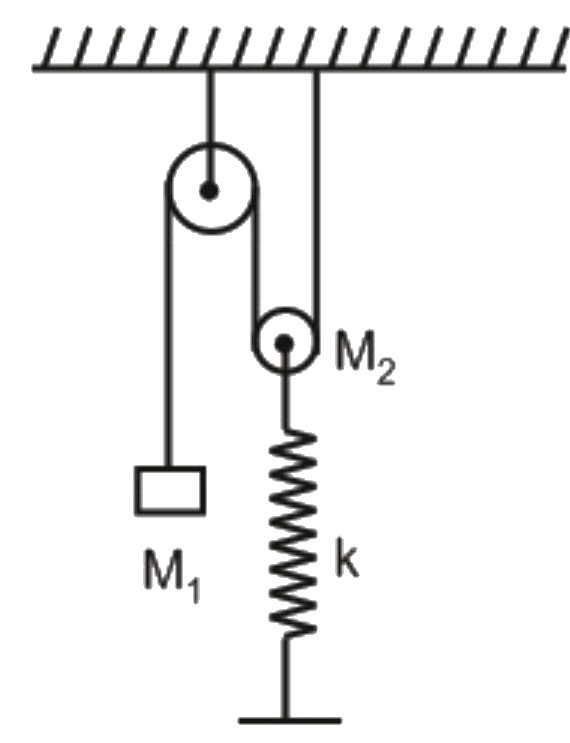
View SolutionA block of mass M1 is constrained to move along with a moveable pulley of mass M2 which is connected to a sprin of force constant k, as shown in the figure. If the mass of the fixed pulley is negligible and friction is absent everywhere, then the period of small oscillations of the system is
View SolutionA 2kg block hangs without vibrating at the bottom end of a spring with a force constant of 400N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5m/s2 when the acceleration suddenly ceases at time t=0 and the car moves upward with constant speed (g=10m/s2)
What is the angular frequencyof the block after the acceleration ceases ?
View SolutionWhen p−n junction diode is forward biased, then
View SolutionA force F is applied on a block of mass 5kg as shown in figure. Co-efficient of friction between the wall and clock is √32.(g=10m/s2)
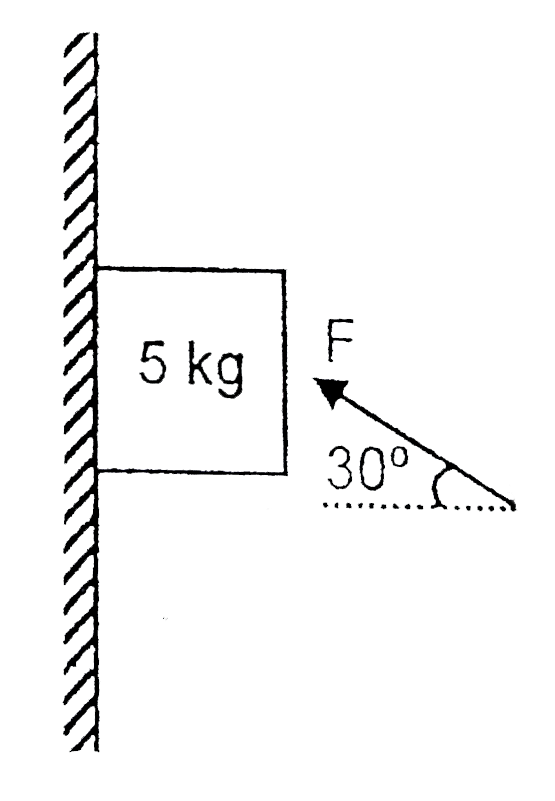
Select correct option(s)
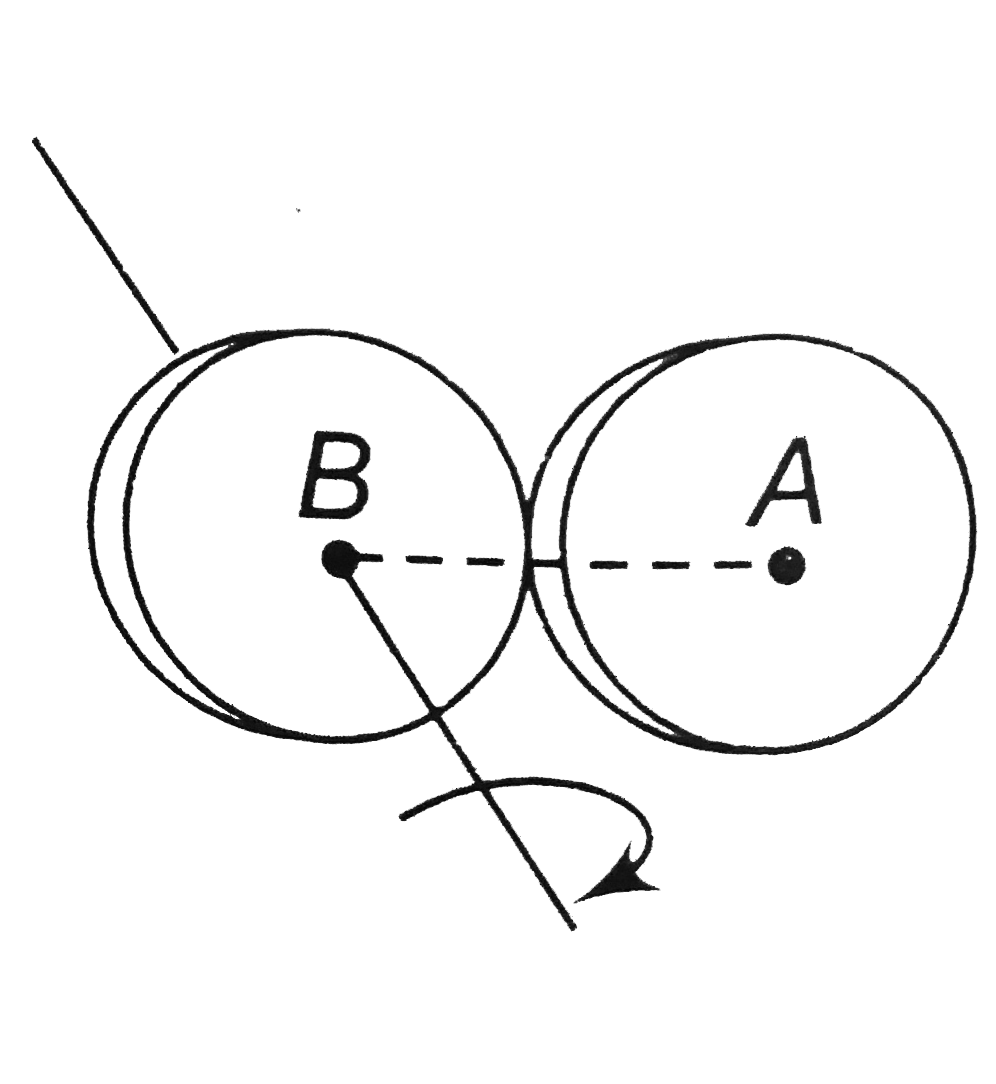
View SolutionTwo thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
 .
.
View SolutionA uniform thin rod of length 1m and mass 3kg is attached to a uniform thin circular disc of radius 30cm and mass 1kg at its centre perpendicular to its plane. The centre of mass of the combination from the centre of disc is
View SolutionA disc of radius a is ridigly attached at its circumference to a rod of length 3a and the combination suspeded vertically from the other end of the rod. It is swinging in the plane of the disc such that the centre of disc has velocity v . If mass of disc and rod is m
View SolutionA uniform disc of mass M and radius R is rotating freely about its central vertical axis with angular speed w0. Another disc of mass m and radius r is free to rotate about a horizontal rod AB. Length of the rod AB isL(<R) and its end A is rigidly attached to the vertical axis of the first disc. The disc of mass m, initially at rest, is placed gently on the disc of mass M as shown in figure. Find the time after which the slipping between the two discs will cease. Assume that normal reaction between the two discs is equal to mg. Coefficient of friction between the two discs is μ.

View SolutionA disc of mass M = 2m and radius R is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre O. A particle of mass m is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.
View SolutionTwo thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
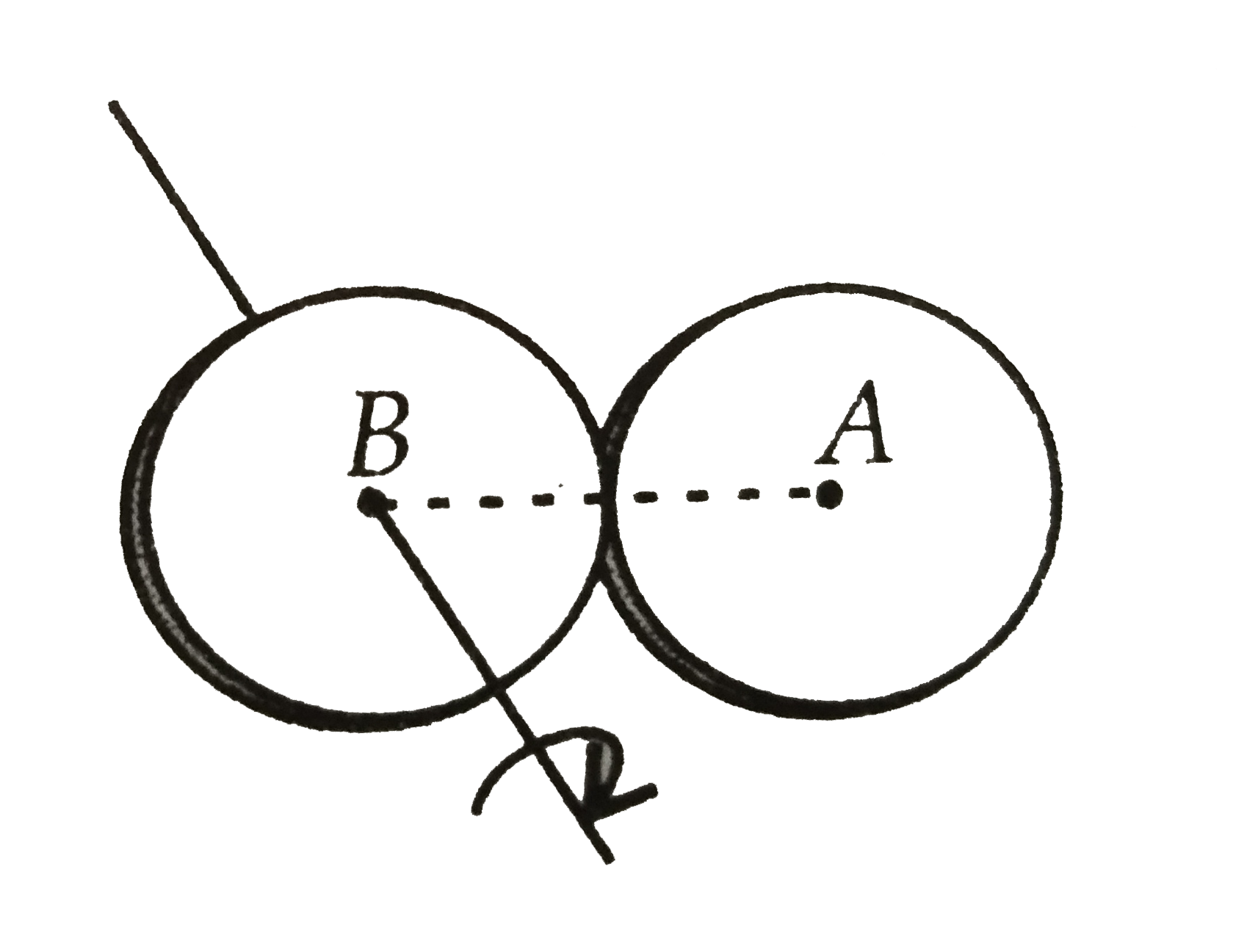
View SolutionA metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R' (lt L) . Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A ). The disc is not free to rotate about its centre and (case B ) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
View SolutionTwo equal and opposite forces are allplied tangentially to a uniform disc of mass M and radius R as shown in the figure. If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :

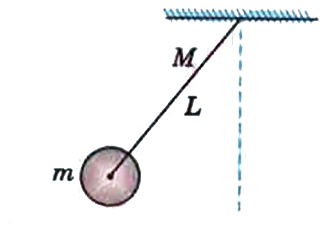
View SolutionOne end of a metal rod of length L and mass M is pivoted to a fixed support and to its free end, a thin disc of mass m and radius r (L) is attached at its centre. In one case, the disc is attached to the rod in such a way that it is not free to rotate about its centre and in another case, teh disc is free to rotate about its centre. When the rod-disc system is displaced slightly from its equilibrium position and released. it peforms S.H.M. in vertical plane. Compare the restoring torque acting on the system and angular frequency in both the cases.
View Solutionलम्बाई 'L' व् द्रव्यमान 'm' की एक धातु चढ़ अपने एक सिरे पर कीलित है। 'R'(<L) त्रिज्या 'M' द्रव्यमान की एक डिस्क छड़ के मुक्त सिरे पर अपने केंद्र से दो तरह से कीलित की जाती है। (स्थिति A ) डिस्क अपने केंद्र पर नहीं घूम सकती और ( स्थिति B ) डिस्क अपने केंद्र पर घूमने को स्वतंत्र है। एक ही विस्थापन अवस्था से छोड़ने पर यह छड़ डिस्क निकाय ऊर्ध्वाधर तल में सरल आवर्त दोलन (SHM ) करता है |तब
View SolutionTwo thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
View Solution
