Using the expression 2dsinθ=λ , one calculates the values of d by measurinf the corresponding angles θ in the range 0∘→90∘. The wavelength λ is exactly known and the error in θ is constant for all values of θ is constant for all the values of θ . As θ increases from 0∘ ,
the absolute error in d remains constant.
the absolute error in d increses.
the fractional error in d remains constant.
the fractional error in d decreases.
The correct Answer is:D
2dsinθ=λ
d=λ2sinθ
differntiate
∂(d)=λ2∂(cosecθ)
∂(d)=λ2(−cosesθcotθ)∂θ
∂(d)=−λcosθ2sin2θ∂θ
as θ=increases,λcosθ2sin2θ,decreases
Alternate solution
d=λ2sinθ
lnd=lnλ−ln2−lnsinθ
Δ(d)d=0−0−1sinθ×cosθ(Δθ)
Fraction error |+(d)|=|cotθΔθ|
Absoulute error Δd=(dcotθ)Δθ
d2sinθ×cosθsinθ
Δd=cosθsin2θ
Topper's Solved these Questions
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise-3 (Part-2)
15 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise-3 (Part-3)
22 Videos
- WAVE OPTICSBOOK - RESONANCE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Exercise-2 (Part-4)
8 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART II
7 Videos
Similar Questions
Young's double slit experiment uses a monochromatic source of light. The shape of interference fringes formed on the screen is
View SolutionIn a cyclotron, a charged particle
View SolutionHuygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
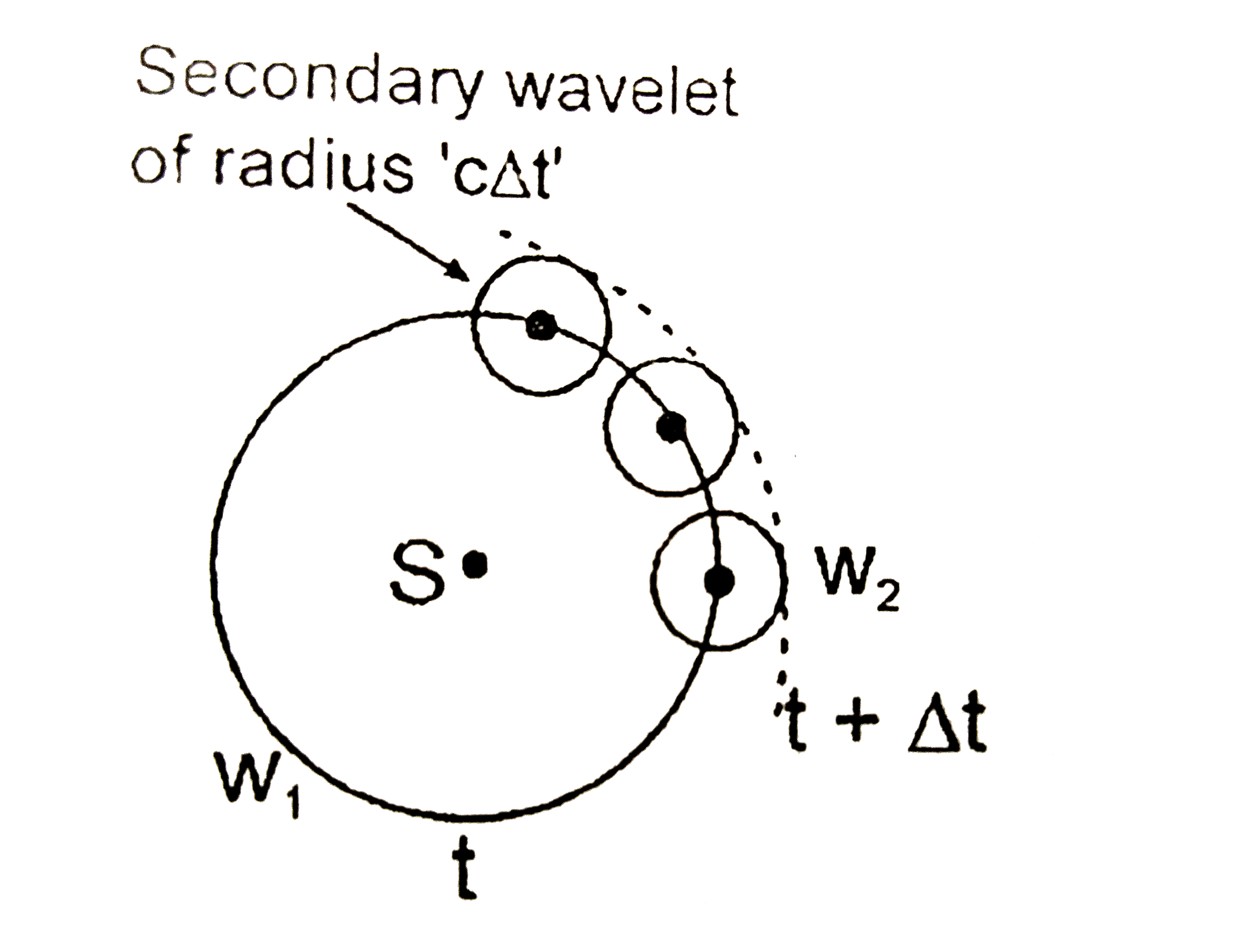
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View Solution(tan theta+cot theta)/(tan theta-cot theta)=2,(0<=theta<=90^(@)) then the value of sin theta is
View SolutionIf A=[cosθsinθ−sinθcosθ]andA(adjA)=λl, then the value of λ is
View SolutionUsing the expression 2d sin theta = lambda , one calculates the values of d by measuring the corresponding angles theta in the range 0 to 90@ . The wavelength lambda is exactly known and error in theta is constant for all values of theta . As theta increases from 0@
View SolutionAs θ increases from 0∘ to 90∘, the value of cosθ is
View SolutionAs θ increases from 0∘ to 90∘, the value of cosθ : -
View Solutionव्यंजक 2dsinθ=λ . प्रयुक्त करने पर, संगत कोण 0, 0 से 90° के range में नापकर कोई d का मान ज्ञात करता है। तरंगदैर्घ्य 2. सही ज्ञात है तथा 0 में त्रुटि 0 के सभी मानों के लिये नियत है। जैसे ही 0, 0 से बढ़ता है :
View Solutionयदि 0∘<θ<90∘ हो तो θ के किस मान के लिए sinθ और cosθ के मान समान होंगे ?
View SolutionIf the equation cos (λsinθ)=sin(λcosθ) has a solution in [0,2π], then the smallest value of λ, is
View SolutionIf sin6θ+cos6θ−1=λsin2θcos2θ then the value of λ is
View SolutionIf maximum and minimum values of 2+2sin2θ for all real values of θ are λ and μ respectively, then λ+ μ=
View Solutionयदि (1+sinθ−cosθ1+sinθ+cosθ)2=λ(1−cosθ1+cosθ) तो λ का मान है
View SolutionIf 0∘<θ<90∘, then the value of sinθ+cosθ is
View Solution

