A light source, which emits two wavelength λ1=400nm and λ2=600nm, is used in a Young's double slit experiment. If recorded fringe width for λ1 and λ2 are β1 and β2 and the number of fringes for them within a distance y on one side of the central maximum are m1 and m2 respectively, then
β2>β1
m1>m2
Form the central maximum, 3rd maximum of λ2 overlaps with 5th minimum of λ1
The angular separation of fringes for λ1 is greater than λ2
The correct Answer is:A, B, C
To solve the problem, we will analyze the given information about the Young's double slit experiment with two different wavelengths of light.
Step 1: Understanding Fringe Width
The fringe width (β) in a Young's double slit experiment is given by the formula:
β=nλDd
where:
- n is the order of the fringe,
- λ is the wavelength of light,
- D is the distance from the slits to the screen,
- d is the distance between the slits.
Step 2: Comparing Fringe Widths
Given:
- λ1=400nm
- λ2=600nm
Since fringe width is directly proportional to the wavelength, we can conclude:
β1<β2
This means that the fringe width for λ1 is less than that for λ2.
Step 3: Number of Fringes
The number of fringes (m) that can fit within a certain distance y on one side of the central maximum is given by:
m=yβ
Since β2>β1, it follows that:
m1>m2
This means that more fringes can fit for the shorter wavelength λ1 compared to the longer wavelength λ2.
Step 4: Overlapping of Maxima and Minima
To check if the third maximum of λ2 overlaps with the fifth minimum of λ1, we need to calculate their positions.
1. Position of Third Maximum for λ2:
y3,λ2=3β2=3(600nm⋅Dd)=1800nm⋅Dd
2. Position of Fifth Minimum for λ1:
The position of the nth minimum is given by:
yn,λ1=(n−12)β1
For the fifth minimum:
y5,λ1=(5−12)β1=92β1=92(400nm⋅Dd)=1800nm⋅Dd
Since both positions are equal:
y3,λ2=y5,λ1
This confirms that the third maximum of λ2 overlaps with the fifth minimum of λ1.
Step 5: Angular Separation
The angular separation θ is given by:
θ=λd
Since λ2>λ1, it follows that:
θ2>θ1
This means that the angular separation for λ2 is greater than that for λ1.
Conclusion
Based on the analysis:
- β2>β1 (Correct)
- m1>m2 (Correct)
- The third maximum of λ2 overlaps with the fifth minimum of λ1 (Correct)
- θ1<θ2 (Incorrect)
Thus, options A, B, and C are correct, while option D is incorrect.
The fringe width (β) in a Young's double slit experiment is given by the formula:
β=nλDd
where:
- n is the order of the fringe,
- λ is the wavelength of light,
- D is the distance from the slits to the screen,
- d is the distance between the slits.
Given:
- λ1=400nm
- λ2=600nm
β1<β2
This means that the fringe width for λ1 is less than that for λ2.
The number of fringes (m) that can fit within a certain distance y on one side of the central maximum is given by:
m=yβ
Since β2>β1, it follows that:
m1>m2
This means that more fringes can fit for the shorter wavelength λ1 compared to the longer wavelength λ2.
To check if the third maximum of λ2 overlaps with the fifth minimum of λ1, we need to calculate their positions.
y3,λ2=3β2=3(600nm⋅Dd)=1800nm⋅Dd
The position of the nth minimum is given by:
yn,λ1=(n−12)β1
For the fifth minimum:
y5,λ1=(5−12)β1=92β1=92(400nm⋅Dd)=1800nm⋅Dd
y3,λ2=y5,λ1
This confirms that the third maximum of λ2 overlaps with the fifth minimum of λ1.
The angular separation θ is given by:
θ=λd
Since λ2>λ1, it follows that:
θ2>θ1
This means that the angular separation for λ2 is greater than that for λ1.
Based on the analysis:
- β2>β1 (Correct)
- m1>m2 (Correct)
- The third maximum of λ2 overlaps with the fifth minimum of λ1 (Correct)
- θ1<θ2 (Incorrect)
Topper's Solved these Questions
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Exercise-3 (Part-2)
Explore 15 Videos
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Exercise-3 (Part-3)
Explore 22 Videos
- WAVE OPTICSBook:RESONANCE ENGLISHChapter:WAVE OPTICSExercise:Exercise-2 (Part-4)
Explore 8 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 3 PART II
Explore 7 Videos
Similar Questions
Young's double slit experiment uses a monochromatic source of light. The shape of interference fringes formed on the screen is
View SolutionIn a cyclotron, a charged particle
View SolutionHuygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
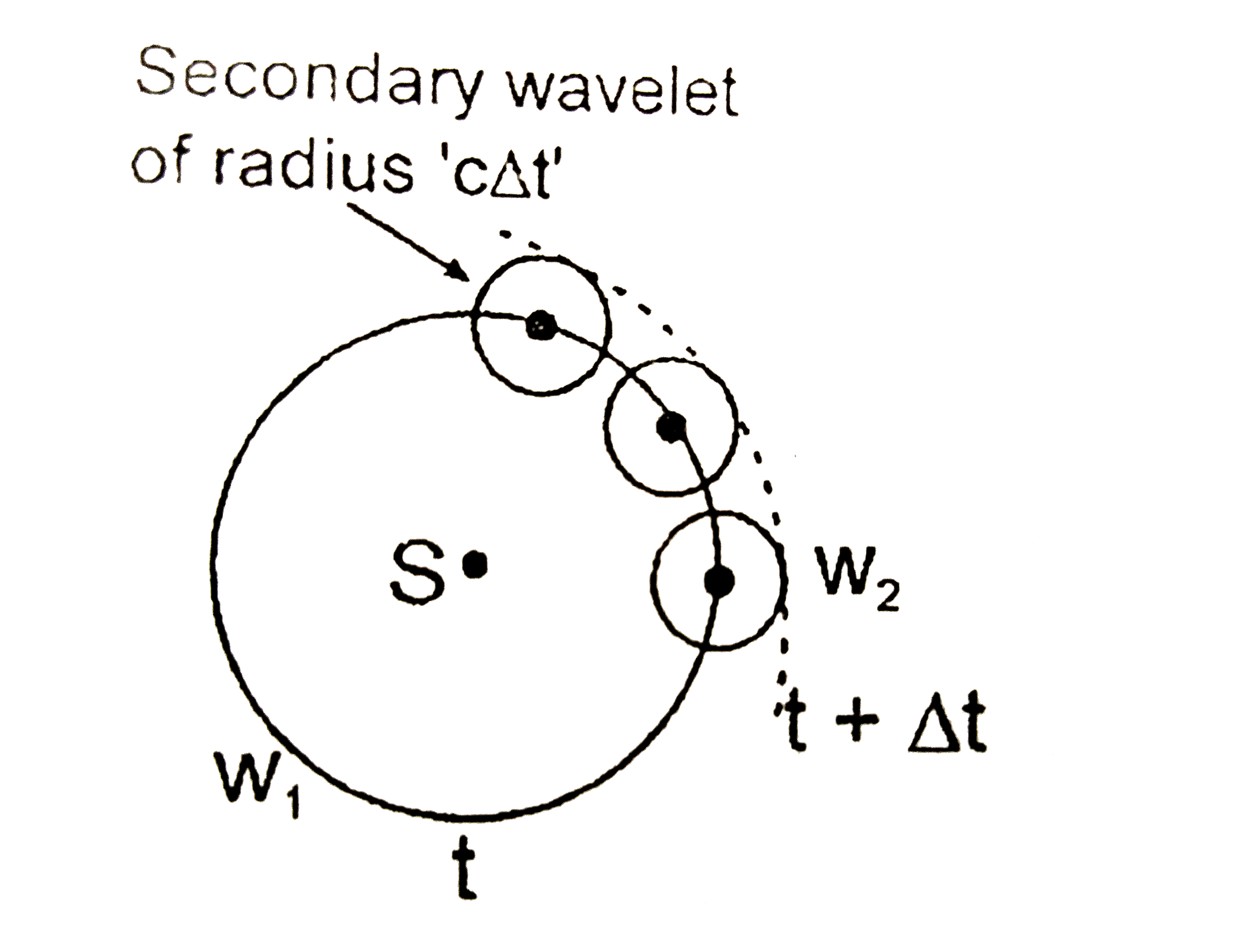
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)
View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionA light source, which emits two wavelength λ1=400nm and λ2=600nm, is used in a Young's double slit experiment. If recorded fringe width for λ1 and λ2 are β1 and β2 and the number of fringes for them within a distance y on one side of the central maximum are m1 and m2 respectively, then
View SolutionA dye absorbs a photon of wavelength lamda and re-emits the same energy into two photns of wavelength lamda_(1) and lamda_(2) respectively. The wavelength lamda is related to lamda_(1) and lamda_(2) as :
View SolutionIn a Young's double slit experiment with slit separation 0.1 mm, one observes a bright fringe at angle 140 rad by using light of wavelength λ1. When the light of wavelength λ2 is used a bright fringe is seen at the same at the same angle in the same set up. Given that λ1andλ2 are in visible range (380 nm to 740 nm), their values are :
View SolutionIn a Young's double slit experiment with slit separation 0.1 mm, one observes a bright fringe at angle 140 rad by using light of wavelength λ1. When the light of wavelength λ2 is used a bright fringe is seen at the same at the same angle in the same set up. Given that λ1andλ2 are in visible range (380 nm to 740 nm), their values are :
View SolutionThe matrix A=⎡⎢ ⎢⎣λ21λ1λ2λ1λ3λ2λ1λ22λ2λ3λ3λ1λ3λ2λ23⎤⎥ ⎥⎦ is idempotent if λ21+λ22+λ23=k where λ1,λ2,λ3 are non-zero real numbers. Then the value of (10+k)2 is . . .
View SolutionIf λ1andλ2 are the wavelengths of the first members of the Lyman and Paschen series respectively, then λ1:λ2 is
View SolutionFor Balmer series, wavelength of first line is lamda_(1) and for Brackett series, wavelength of first line is lamda_(2) then (lamda_(1))/(lamda_(2))
View SolutionIn Young's double slit experiment, two wavelength λ1=780nm and λ2=520 nm are used to obtain interference fringes. If the nth bright band due to λ1 coincides with (n+1)th bright band due to λ2 then the value of n is
View Solutionयंग के द्विछिद्री प्रयोग में प्रयुक्त प्रकाश स्रोत दो तरंगदैर्ध्यों λ1=400nm तथा λ2=600nm को उत्सर्जित करता है | यदि तरंगदैर्ध्यों λ1 तथा λ2 के लिए अभिलिखित फ्रिंज चौड़ाइयाँ क्रमशः β1 तथा β2 हैं, तथा केंद्रीय दीप्त फ्रिंज के एक ओर y दूरी तक फ़्रिंजों की संख्या क्रमशः m1 तथा m2 हैं, तब
View Solutionlamda_(1) and lamda_(2) are used to illuminated the slits. beta_(1) and beta_(2) are the corresponding fringe widths. The wavelength lamda_(1) can produce photoelectric effect when incident on a metal. But the wavelength lamda_(2) cannot produce photoelectric effect. The correct relation between beta_(1) and beta_(2) is
View Solutionλ1 and λ2 are used to illuminated the slits. β1 and β2 are the corresponding fringe widths. The wavelength λ1 can produce photoelectric effect when incident on a metal. But the wavelength λ2 cannot produce photoelectric effect. The correct relation between β1 and β2 is
View Solution
