A sonometer wire when vibrated in full length has frequency n. Now, it is divided by the help of bridges into a number of segments of lengths l1,l2,l3… when vibrating these segments have frequencies n1,n2,n3,,, Then, the correct relation is
n=n1+n2+n3+…..
n+√n1×n2×n3×….
1n=1n1+1n2+1n3+…..
none of the above
The correct Answer is:C
n1=v2l1,n2=v2l2
and n=v2l (for complete lenglth of wire)
As l=l1+l2+….
V2n=V2n1+V2n2+….
1n=1n1+1n2+…

Topper's Solved these Questions
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 2 PART II
Explore 19 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 2 PART III
Explore 15 Videos
- TRAVELLING WAVESBook:RESONANCE ENGLISHChapter:TRAVELLING WAVESExercise:Exercise- 1 PART II
Explore 30 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
- WAVE ON STRING Book:RESONANCE ENGLISHChapter:WAVE ON STRING Exercise:Exercise- 3 PART II
Explore 7 Videos
Similar Questions
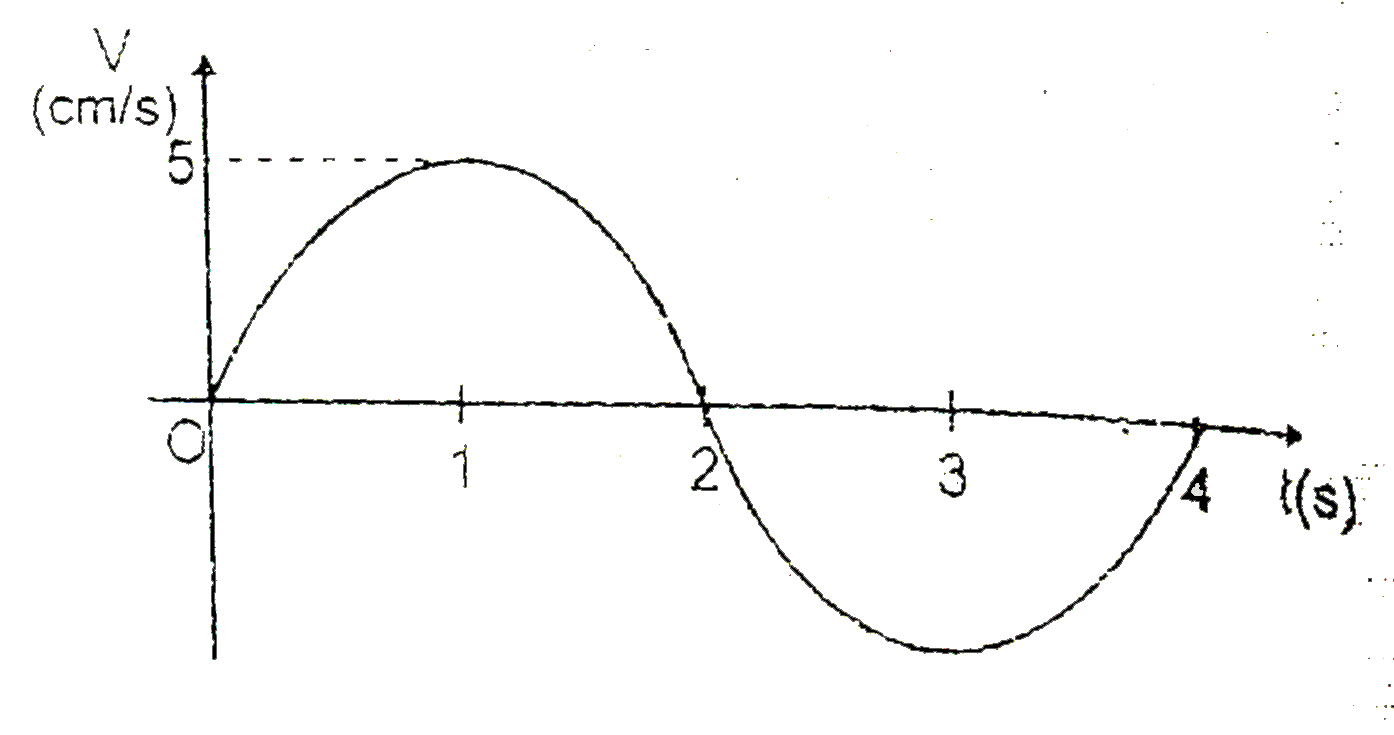
A certain transvers sinusoidal wave of wavelength 20cm is moving in the positive X direction. The transverse velocitt of the particle at x=0 as a function of time is shonwn. The amplitude of the motion is equal to xπ (in cm). Find x :
View SolutionThe plane wave represented by an eqution of the form y = f(x-vt) implies the propagation along the positive x-axis without chang of shape with constant velocity v. Then
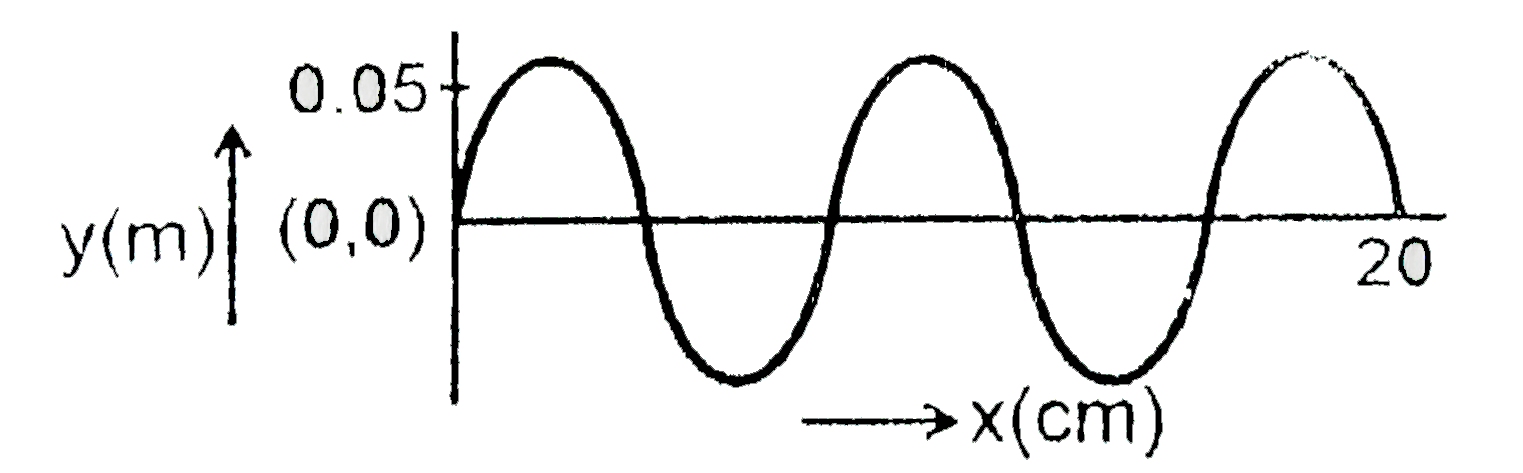
View SolutionFor the wave shown in figure, the equation for the wave, travelling along +x acis with velocity 350ms−1 when its position at t=0 is as shown
View SolutionA time varying voltage is applied across A & B such that voltage across capacitor is given by VC=2sin2t. What is maximum potential difference across the reistance?

View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionA sonometer wire when vibrated in full length has frequency n. Now, it is divided by the help of bridges into a number of segments of lenths l_(1),l_(2),l_(3)… when vibration these segments have frequencies n_(1), n_(2), n_(3),,, Then, the correct relation is
View SolutionA sonometer wire is divided in many segments using bridges. If fundamental natural frequencies of the segments are n_(1), n_(2), n_(3)….. then the fundamental natural frequency of entire sonometer wire will be (if the divisons were not made):
View SolutionIn a pipe opened at both ends n_(1) and n_(2) be the frequencies corresponding to vibrating lengths L_(1) and L_(2) respectively .The end correction is
View SolutionWhen a string is divided into three segments of lengths l_(1),l_(2) and l_(3) the fundamental frequencies of these three segments are v_(1), v_(2) and v_(3) respectively. The original fundamental frequency (v) of the string is
View SolutionIn a pipe opened at both ends n_(1) and n_(2) be the frequencies corresponding to vibrating lengths L_(1) and L_(2) respectively .The end correction is
View Solutionयदि (l1,m1,n1),(l2,m2,n2) और (l3,m3,n3) तीन परस्पर लब सरल रेखाओ की दिककोज्याए हो , तो सिद्ध कीजिए की l1m2n2−m3n2=m1n2l3−n3l2=n1l2m3−l3m2=±1]
View SolutionA thin wire of length of 99 cm is fixed at both ends as shown in the figure. The wire is kept under a tansion and is divided into three segments of lenghts l_(1)l_(2) and l_(3) as shown in figure. When the wire is made to vibrate, the segments vibrate respectively in the ratio 1 : 2 : 3, Then, hte lenghts l_(1),l_(2) and l_(3) of the segments respectively are (in cm)
View SolutionA thin wire of length of 99 cm is fixed at both ends as shown in the figure. The wire is kept under a tension and is divided into three segments of lengths 1, 1, and I, as shown in figure. When the wire is made to vibrate, the segments vibrate respectively with their fundamental frequencies in the ratio 1:2:3. Then, lengths l1,l2,l3 of the segments respectively are (in cm)

View SolutionWhen a string is divided into three segments of length l1,l2,andl3 the fundamental frequencies of these three segments are v1,v2andv3 respectively .
The original fundamental frequency (v) of the string is
View SolutionAn addiditional bridge is kept below a sonometer wire so that it is divided into two segments of lengths in the ratio 2 : 3 and n_(1) , n_(2) are their respective fundamental frequencies. If the additional bridge is removed then the fundamental frequency of that sonometer wire is n, the ratio of n,n_(1),n_(2) is
View SolutionThe frequencies of a pipe which is open at both ends respectively n_(1) And n_(2) And generated staggered lengths l_(1) And l_(2) is. Their final modification is.
View Solution
