A string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of same small length at positions l1=0.2Landl2=0.45L from one end. If K1 and K2 are their respectived maximum kinetic energies then \
K1=K2
K1>K2
K1<K2,
It is not possible to decide the relation.
The correct Answer is:B
Step by step video solution for A string of length L, fixed at its both ends is vibrating in its 1^(st) overtone mode. Consider two elements of the string of same small length at positions l_(1)=0.2 L and l_(2) = 0.45 L from one end. If K_(1) and K_(2) are their respectived maximum kinetic energies then \ by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 2 PART II
19 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 2 PART III
15 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 1 PART II
30 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART II
7 Videos
Similar Questions
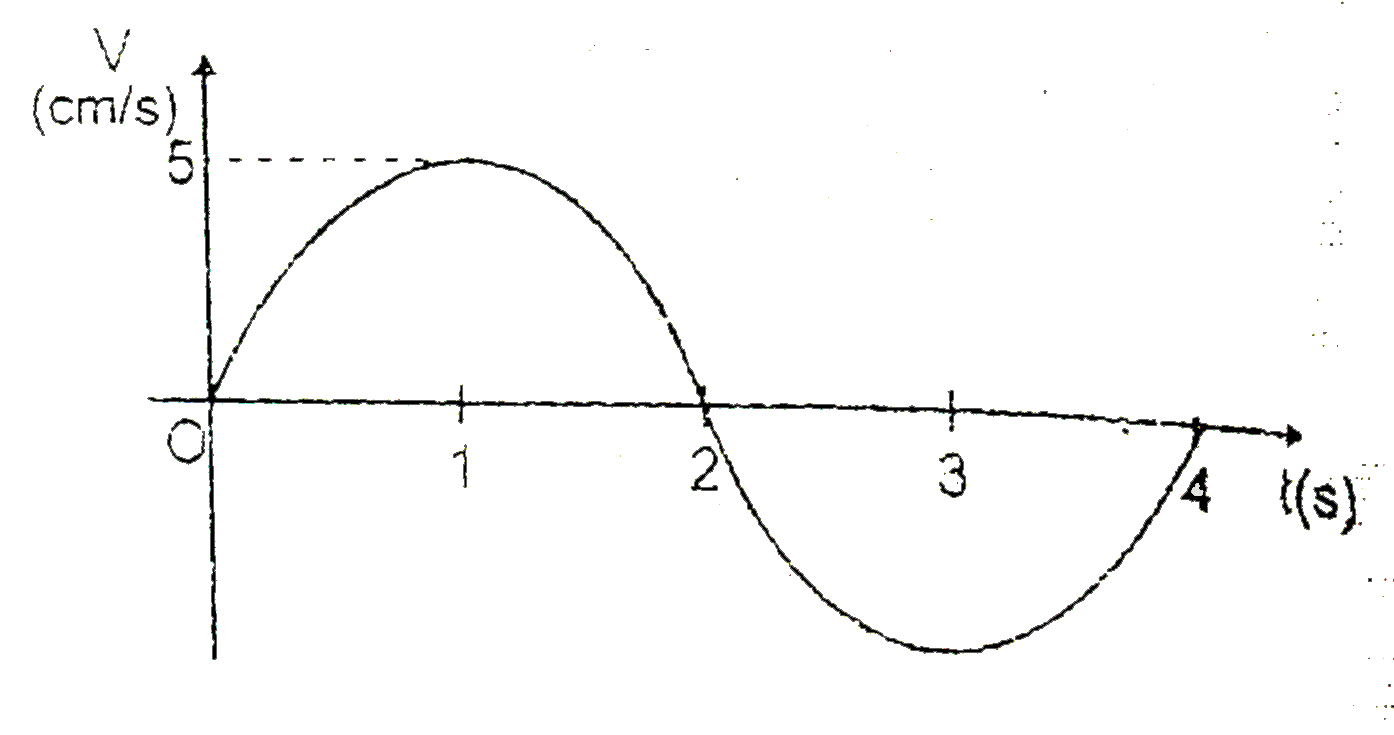
A certain transvers sinusoidal wave of wavelength 20cm is moving in the positive X direction. The transverse velocitt of the particle at x=0 as a function of time is shonwn. The amplitude of the motion is equal to xπ (in cm). Find x :
View SolutionThe plane wave represented by an eqution of the form y = f(x-vt) implies the propagation along the positive x-axis without chang of shape with constant velocity v. Then
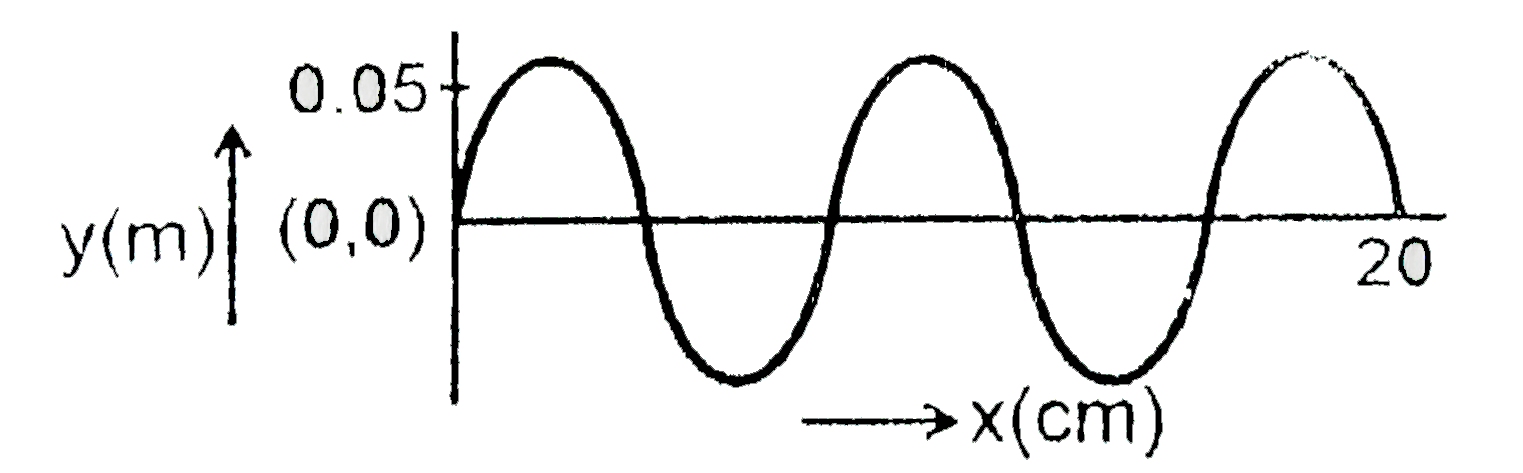
View SolutionFor the wave shown in figure, the equation for the wave, travelling along +x acis with velocity 350ms−1 when its position at t=0 is as shown
View SolutionA time varying voltage is applied across A & B such that voltage across capacitor is given by VC=2sin2t. What is maximum potential difference across the reistance?

View SolutionA string is stretched betweeb fixed points separated by 75.0cm. It observed to have resonant frequencies of 420Hz and 315Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for this strings is
View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l_(1) and l_(2) . If their respective spring constahnt are K_(1) and k_(2) , then (K_(1))/(K_(2)) is:
View SolutionA string of length 'l' is fixed at both ends. It is vibrating in its 3rd overtone with maximum ampltiude 'a'. The amplitude at a distance l3 from one end is =√pa2. Find p.
View SolutionA string of length L fixed at its at its both ends is vibrating in its 1^(st) overtone mode. Consider two elements of the string of same small length at position l_1=0.2L and l_2=0.45L from one end. If K_1 and K_2 are their respective maximum kinetic energies then
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionA string of length L, fixed at its both ends is vibrating in its 1^(st) overtone mode. Consider two elements of the string of the same small length at positions l_(1)=0.2L"and"l_(2)=0.45L from one end. Follow situation of part (a) If K_(1) "and" K_(2) are respective force constants of their simple hrmonic motions, then
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionA string of length 'l' is fixed at both ends. It is vibrating in its 3rd overtone with maximum ampltiude 'a'. The amplitude at a distance l3 from one end is =√pa2. Find p.
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionWhen the string of the sonometer of length l between the bridges vibrates in the first overtone, then the antinode formed from one end of the string will be
View SolutionA string of length L fixed at both ends vibrates in its first overtone. Then the wavelength will be
View SolutionA wire of length L is hanging from a fixed support. The length changes to L1andL2 when masses M1andM2 are suspended respectively from its free end. Then L is equal to
View Solution

