N cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
a.Maximum power is delivered to the load is K=√NRr
b.Maximum power is delivered to the load if K=√rNR
c.Maximum power delivered to the load is E24Nr
d.Maximum power deliverd to the load is N(E)24r
The correct Answer is:A, D
To solve the problem, we need to analyze the arrangement of the cells and derive the expressions for the maximum power delivered to the load. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the Configuration
We have N cells, each with an electromotive force (e.m.f.) E and internal resistance r. These cells are grouped into sets of K cells connected in series. Therefore, the total e.m.f. of one set is:
Eset=K⋅E
The total internal resistance of one set of K cells in series is:
rset=K⋅r
Step 2: Finding the Number of Sets
The total number of sets formed is given by:
Number of sets=NK
Step 3: Equivalent Circuit for Sets in Parallel
The sets of K cells are connected in parallel to a load resistance R. The equivalent internal resistance of the sets in parallel can be calculated as follows:
The equivalent resistance Req of the sets in parallel is given by:
1Req=1rset⋅NK=1K⋅r⋅NK=NK2r
Thus, the equivalent internal resistance is:
Req=K2rN
Step 4: Total E.M.F. of the Configuration
The total e.m.f. of the configuration (since all sets are identical) remains:
Etotal=K⋅E
Step 5: Applying Maximum Power Transfer Theorem
According to the maximum power transfer theorem, maximum power is delivered to the load when the load resistance R is equal to the equivalent internal resistance Req:
R=Req=K2rN
Step 6: Solving for K
To find the value of K that maximizes power transfer, we can rearrange the equation:
K2=R⋅Nr
Taking the square root gives:
K=√R⋅Nr
Step 7: Maximum Power Calculation
The maximum power Pmax delivered to the load can be calculated using:
Pmax=E2total(Req+R)2⋅R
Substituting Req=R:
Pmax=(K⋅E)2(2R)2⋅R=K2E24R
Substituting K2 from earlier:
Pmax=R⋅Nr⋅E24R=N⋅E24r
Conclusion
The derived expressions show that the value of K for maximum power transfer is:
K=√R⋅Nr
And the maximum power delivered to the load is:
Pmax=N⋅E24r
We have N cells, each with an electromotive force (e.m.f.) E and internal resistance r. These cells are grouped into sets of K cells connected in series. Therefore, the total e.m.f. of one set is:
The total number of sets formed is given by:
The sets of K cells are connected in parallel to a load resistance R. The equivalent internal resistance of the sets in parallel can be calculated as follows:
The total e.m.f. of the configuration (since all sets are identical) remains:
According to the maximum power transfer theorem, maximum power is delivered to the load when the load resistance R is equal to the equivalent internal resistance Req:
To find the value of K that maximizes power transfer, we can rearrange the equation:
The maximum power Pmax delivered to the load can be calculated using:
The derived expressions show that the value of K for maximum power transfer is:
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-4)
12 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exrcies-3(PART-1)
22 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-2)
16 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Video
Similar Questions
In the circuit given in the figure, both batteries are ideal . Emf E1 of battery 1 has a fixed value, but emf E2 of battery 2 can be varied between 1.0Vand10.0V . The graph gives the currents through the two batteries as a function of E2 but are not marked as which plot corresponds to which battery. But for both plots, current is assumed to be negative when the direction of the current through the battery is opposite to the direction of that battery's emf (direction of emf is from negative to positive.)
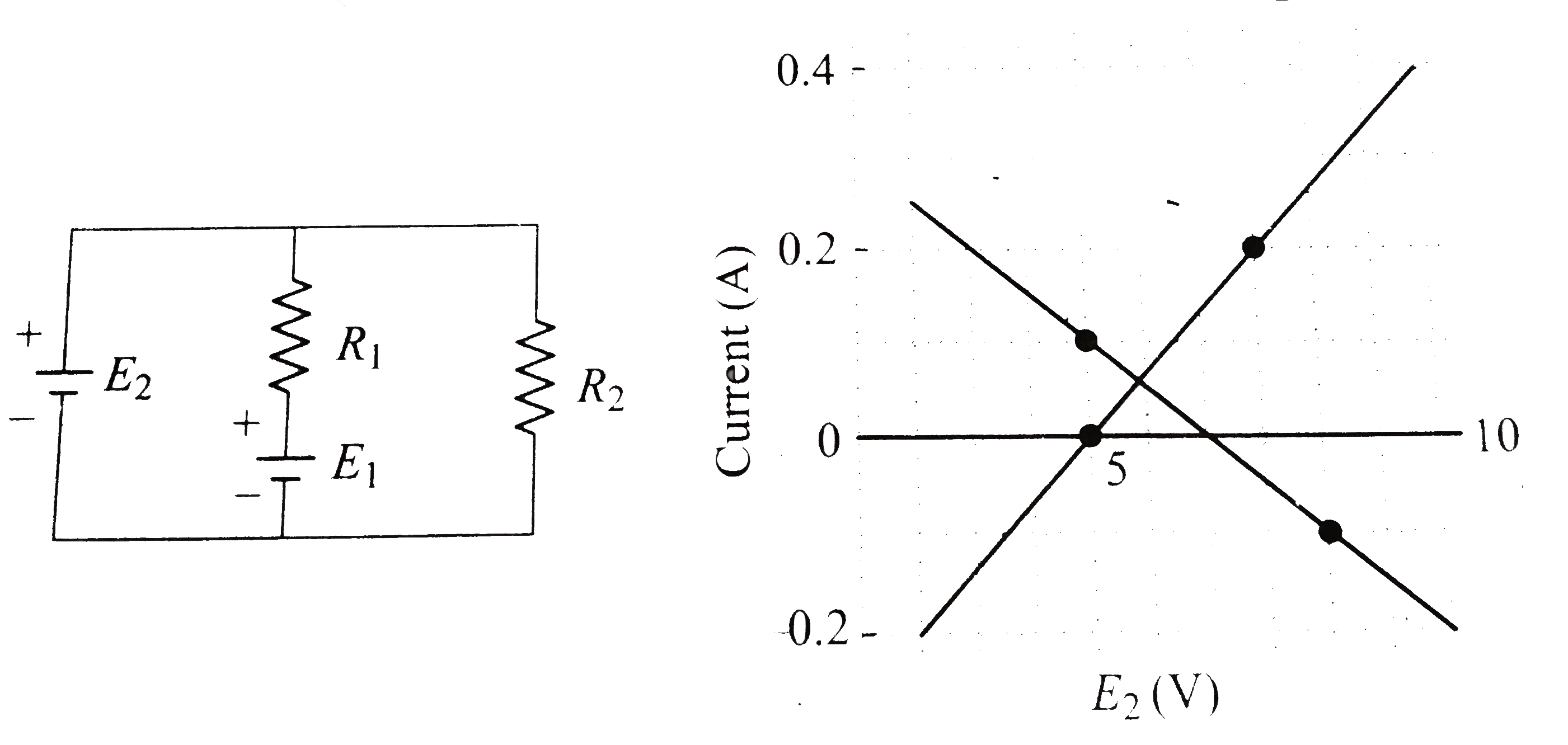
The value of emf E1 is
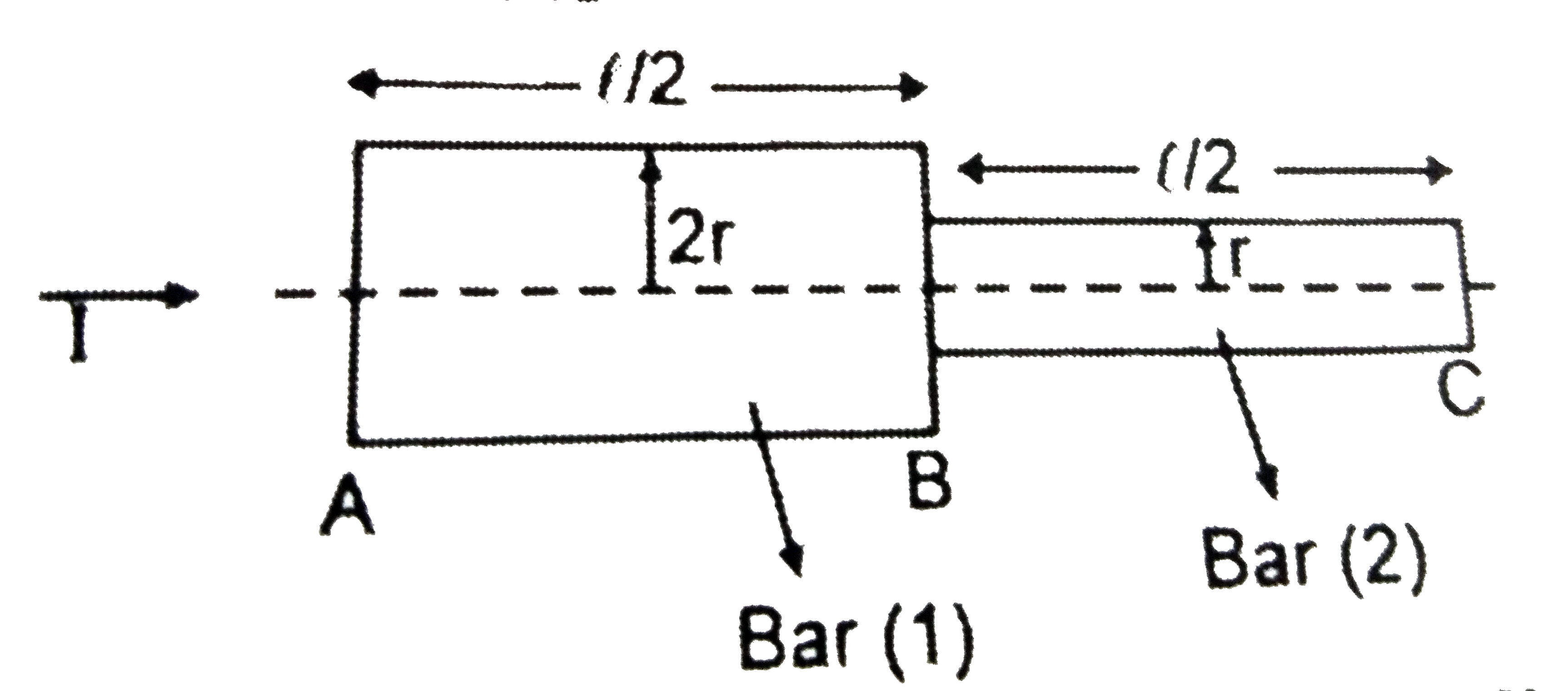
View SolutionTwo bars of equal resistivity ρ and radius 'r' and '2r' are kept in contact as show. An electric current is passed through the bars. Which one of the following is correct ?
View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r=0) and decreases linearly to zero at the surface (r=R). Calculate the current in terms of J0 and the conductor's cross - sectional area A=πR2.
View SolutionConsider telecommunication through optical fibers. Which of the following statements is not true ?
View SolutionConsider a uniform wire of length l. Cross-sectional area A, Young's modulus of the material of the wave is Y. Some information related to the wire is given in column-1 and dependence of the result is given in column-2. Then match the approprite choice between the columns and match the list given in options
Column-I Column-II(A) Let us suspend wire vertically from a (p) Young'sModulusrigud support and attach a mass m atits lower end. If the mass is slightly pulleddown and released, it executes S.H.Mof a time period which will depend on(B) Work done in stretching the wire up to length (q) elongation (x)l+xwill depend on(C) If the given is fixed between two rigid (r) length (l)supports and its temperature is decreasedthermal stress that develops in the wirewill depend on(D) If the wire is pulled at its ends equal and (s) area of cross-section (A) opposite forces of magnitude F so that itundergoes an elongation x, according toHook's law, F=kx, where k is the forceconstant.Force constant (k) of the wirewill depend on
View SolutionA cell of e.m.f. E is connected with an external resistance R , then p.d. across cell is V . The internal resistance of cell will be
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionN identical cells whether joined together in series or in parallel, give the same current, when connected to an external resistance of 'R'. The internal resistance of each cell is:-
View SolutionN cells each of e.m.f. E & internal resistance r are grouped into sets of K cells connected in series. The (N/K) sets ae connected in parallel to a load of resistance R, then,
View SolutionA cell of e.m.f (E) and internal resistance (r) is connected in series with an external resistance (nr.) then the ratio of the terminal p.d. to E.M.F is
View SolutionFive cells each of e.m.f E and internal resistance r are connected in series. If due to over sight, one cell is connected wrongly ,the equivalent e.m.f of the combination is
View SolutionThere are N identical cells of emf E and internal resistance r connected in series with each other. But n cells are connected with reverse polarity and n lt N//2 . Effective emf and internal resistance of this combination are
View Solutionn identical cells each of emfE and internal resistance r are connected in series. An external resistance R is connected in series with this combination.The current through R is :
View Solutionn number of cells e.m.f of each is E and internal resistance is r connected in parallel or series combination and are connect to external resistance R.Same current flows through R in both cases. Then—
View SolutionA circuit consists of a resistance R connected to n similar cells. If the current in the circuit is the same whether the cells are .connected in series or in parallel, then the internal resistance r of each cell is given by
View Solution

