Consider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume u=UV∝T4 and pressure p=13(UV). If the shell now undergoes an adiabatic expansion the relation between T and R is :
T∝s−R
T∝S−3R
T∝1R
T∝1R3
The correct Answer is:C
According to equestion,
p=13(UV)⇒nRTV=13(UV) [∴Pv=nRT]
or nRTV∝13T4 or VT3= constant or 43πR3T3= constant or TR= constant ⇒T∝1R.
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
109 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - Level - 2
40 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Video
Similar Questions
An ideal gas is taken around the cycle ABCDA as shown in the P-V diagram. What is the work done during the cycle?
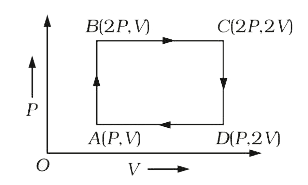
View SolutionA closed vessel of fixed volume contains a mass m of an ideal gas, the root mean square speed being v. Additional mass m of the same gas is pumped into the vessel and the pressure rises to 2P, the temperature remaining the same as before. The root mean square speed of the molecules now is :
View SolutionTwo particles of mass 1 kg and 3 kg move towards each other under their mutual force of attraction. No other force acts on them. When the relative velocity of approach of the two particles is 2m/s, their centre of mass has a velocity of 0.5 m/s. When the relative velocity of approach becomes 3m/s, the velocity of the centre of mass is 0.75 m/s.
View SolutionIs it possible to put an artificial satellite in an orbit in such a way that it always remain visible directly over New Delhi ?
View SolutionConsider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume u=UV∝T4 and pressure P=13(UV). If the shell now undergoes an adiabatic expansion the relation between T and R is :
View Solutionकिसी गोलीय कोष (शेल) की त्रिज्या R है और इसका ताप T है। इसके भीतर कृष्णिका विकीरणों को फोटॉनों की एक ऐसी आदर्श गैस माना जा सकता है जिसकी प्रति एकांक आयतन आन्तरिक ऊर्जा, u=UV∝T4 तथा दाब P=13(UV) है। यदि इस कोष में रुद्धोष्म प्रसार हो तो, T तथा R के बीच सम्बन्ध होगा :
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T prop V^(-(3)/(4)) , then the value of (C_(P))/(C_(V)) for the gas is
View SolutionAn ideal gas (whose CpCv=λ, and internal energy U at absolute zero temp. is equal to zero) undergoes a reversible adiabatic compression. If U,p,V,T Represent the internal energy, pressure, volume and temperature respectively of the ideal gas, then
View SolutionPlot a graph between internal energy U and Temperature (T) of an ideal gas.
View SolutionConsider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit colume u=(U)/(V)propT^(4) and pressure P=1/3((U)/(V)) . If the shell now undergoes an adiabatic expansion the relation between T and R is :
View SolutionThe temperature of a spherical shell of radius R is T. The black mass radiation inside it can be considered as an ideal photon gas with u energy per unit volume (u = U / V prop T ^ 4) with a pressure of 1/3 (U / V). Now the relation of T and R will be when the heat of the creator expands
View Solutionकिसी गोलीय कोष (शेल) की त्रिज्या R है और इसका ताप T है। इसके भीतर कृष्णिका विकीरणों को फोटॉनों की एक ऐसी आदर्श गैस माना जा सकता है जिसकी प्रति एकांक आयतन आन्तरिक ऊर्जा, u=UV∝T4 तथा दाब P=13(UV) है। यदि इस कोष में रुद्धोष्म प्रसार हो तो, T तथा R के बीच सम्बन्ध होगा :
View SolutionConsider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume u=UV∝T4 and pressure P=13(UV). If the shell now undergoes an adiabatic expansion the relation between T and R is :
View SolutionThe internal energy (U), pressure (P) and volume (V) of an ideal gas are related as U=3PV+4. The gas is :-
View SolutionConsider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume u=U/V propT^4 and pressure P=1/3(U/V) . If the shell now undergoes an adiabatic expansion the relation between T and R is :
View SolutionThe internal energy (U) ,pressure (P) and volume V of an ideal gas are related as U=3PV+4 .The gas is
View Solution

