The locus of the mid-points of the chords of the circle of lines radiùs r which subtend an angle π4 at any point on the circumference of the circle is a concentric circle with radius equal to (a) r2 (b) 2r3 (c) r√2 (d) r√3
x2+y2=1
x2+y2=274
x2+y6(2)=94
x2+y2=32
The correct Answer is:C
Let P(h,k) be the mid-point of the chord subtending angle 2π3 at the centre.
In ΔOPA, we have
cos(π)3=OPOA
⇒2OP=OA
⇒4OP2=OA2
⇒4(h2+k2)=9
∴Locus of (h,k) is x2+y2=94.
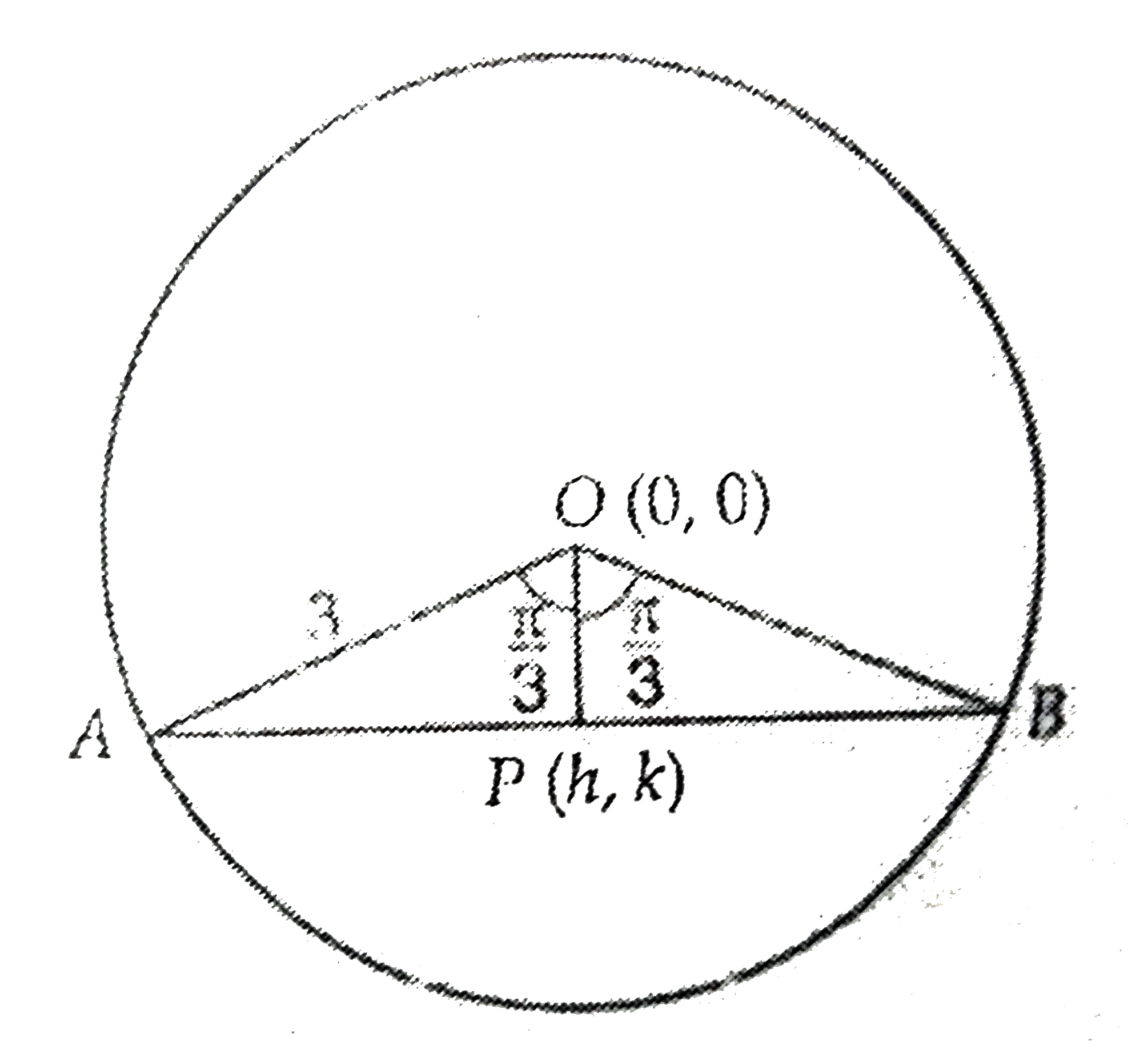
Topper's Solved these Questions
- CIRCLESBook:OBJECTIVE RD SHARMA ENGLISHChapter:CIRCLESExercise:Section-I (Solved MCQs)
Explore 1 Video
- CIRCLESBook:OBJECTIVE RD SHARMA ENGLISHChapter:CIRCLESExercise:Section II - Assertion Reason Type
Explore 12 Videos
- CIRCLESBook:OBJECTIVE RD SHARMA ENGLISHChapter:CIRCLESExercise:Chapter Test
Explore 53 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS Book:OBJECTIVE RD SHARMA ENGLISHChapter:CARTESIAN PRODUCT OF SETS AND RELATIONS Exercise:Chapter Test
Explore 30 Videos
- COMPLEX NUMBERS Book:OBJECTIVE RD SHARMA ENGLISHChapter:COMPLEX NUMBERS Exercise:Chapter Test
Explore 58 Videos
Similar Questions
if one of the diameters of the circle, given by the equation, x2+y2−4x+6y−12=0, is a chord of a circles S, whose centre is at (−3,2) , then the radius of S is
View Solutionabout to only mathematics
View SolutionThe two circles x2+y2−2x+6y+6=0andx2+y2−5x+6y+15=0 touch eachother. The equation of their common tangent is : (A) x=3 (B) y=6 (C) 7x−12y−21=0 (D) 7x+12y+21=0
View SolutionIf n(A×B)=45, then n(A) cannot be
View SolutionThe locus of the center of a circle which touches the circles |z−z1|=a,|z−z2=b| externally will be
View SolutionIn a circle of radius r, chords of length aandbcm subtend angles θand3θ , respectively, at the center. Show that r=a√a3a−bcm
View SolutionThree equal circles each of radius r touch one another. The radius of the circle touching all the three given circles internally is (2+√3)r (b) (2+√3)√3r (2−√3)√3r (d) (2−√3)r
View SolutionThe locus of the mid-points of the chords of the circle of lines radis r which subtend an angle (pi)/(4) at any point on the circumference of the circle is a concentric circle with radius equal to
View SolutionIn Fig. 15.111, if ABC is an equilateral triangle, then shaded area is equal to (FIGURE) (a) (π3−√34)r2 (b) (π3−√32)r2 (c) (π3+√34)r2 (d) (π3+√3)r2
View SolutionTwo equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circles is √r (b) √2 r AB (c) √3 r (d) √32 rLet the two circles have their centres at AandC.
View SolutionFind the equation of the circle in which the chord joining the points (a,b) and (b,-a) subtends an angle of 45^(@) at any point on the circumference of the circle.
View SolutionTwo chords of a circle are of lengths a cm and b cm and they subtend angles θ and 3θ respectively at the center of the circl. If the radius of the circle by r cm, show that,
r=a√a3a−b cm.
View SolutionLet C be the circle with centre (0,0) and radius 3. Show that he equation of the locus of the mid points of the chord of the circle C that subtend an angle 2π3 at its centre is x2+y2=94.
View SolutionThree equal circles each of radius r touch one another. The radius of the circle touching all the three given circles internally is (2+√3)r (b) (2+√3)√3r (2−√3)√3r (d) (2−√3)r
View SolutionThe locus of the mid-points of the chords of the circle of lines radiùs r which subtend an angle π4 at any point on the circumference of the circle is a concentric circle with radius equal to (a) r2 (b) 2r3 (c) r√2 (d) r√3
View SolutionIn Fig. 15.111, if ABC is an equilateral triangle, then shaded area is equal to (FIGURE) (a) (π3−√34)r2 (b) (π3−√32)r2 (c) (π3+√34)r2 (d) (π3+√3)r2
View Solution
