In a right angled ΔABC,∠A=90∘. If AC = b, BC = a, AB = c and r and R are respectively radii of incircle and circumcircle of the triangle then prove that 2(r + R) = b + c
Step by step video solution for In a right angled DeltaABC, angleA=90^(@). If AC = b, BC = a, AB = c and r and R are respectively radii of incircle and circumcircle of the triangle then prove that 2(r + R) = b + c by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6A
59 Videos
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- ALGEBRAIC IDENTITIES BOOK - LUCENT PUBLICATIONCHAPTER - ALGEBRAIC IDENTITIES EXERCISE - Exercise - 1B
28 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
Similar Questions
In the adjacent figure DE is parallel to BC and ratio of areas of ΔADE and trapezium BDEC is 4 : 5. What is the value of DE : BC?
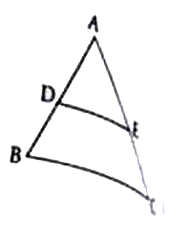
View SolutionIn ΔABC, AD is median and AD = 1/2 BC. If ∠BAD=30∘ then find ∠ACB.
View SolutionIf a+b+1=0 then what is the value of (a3+b3+1−3ab)?
View SolutionTwo tangents are drawn from a point P on the circle at point A and B. O is the centre of the circle. If ∠AOP=60∘ then find ∠APB.
View SolutionIf ABC is isosceles with AB=AC and C(O, r) is the incircle of the ABC touching BC at L , prove that L bisects BC .
View SolutionIn ΔABC,∠C=2∠A,andAC=2BC, then the value of a2+b2c2R2 (where R is circumradius of triangle) is ______
View SolutionLet Δ=∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣ and the equation
x3−px2+qx−r=0 has roots a,b,c, where a,b,c ∈R+
The value of D≤ta is
View SolutionLet Δ=∣∣ ∣ ∣∣−bcb2+bcc2+bca2+ac−acc2+aca2+abb2+ab−ab∣∣ ∣ ∣∣ and the equation
x3−px2+qx−r=0 has roots a,b,c, where a,b,c ∈R+
If a,b,c are in GP then
View SolutionIf r and R are radii of the incircle and circum-circle of ΔABC, then prove that :
8rR{cos2A/2+cos2B/2+cos2C/2}
=2bc+2ca+2ab−a2−b2−c2.
View SolutionIn a right angled ΔABC,∠ACB=90∘. A circle is inscribed in the triangle with radius r, a, b, c are the lengths of the sides BC, AC and AB respectively. Prove that 2r=a+b−c.

View Solutionसिद्ध करे कि ∣∣ ∣ ∣∣−a2abacba−b2bccacb−c2∣∣ ∣ ∣∣≥0 जहाँ a∈R,b∈R,c∈R
View Solutionযদি (nCr−1a)=nCrb=(nCr+1c) হয়, তবে প্রমাণ কর n=ab+2ac+bcb2−ac এবং r=a(b+c)b2−ac
View SolutionIn ΔABC,∠C=2∠A,andAC=2BC, then the value of a2+b2c2R2 (where R is circumradius of triangle) is ______
View SolutionΔABC the lengths of sides AC and AB are 12 cm and 5 cm, respectively. If the area of ΔABC is 30 cm2 and R and r are respectively the radii of circumcircle and incircle of ΔABC then the value of 2R+r (in cm) is equal to......
View SolutionIf r and R are radii of the incircle and circum-circle of ΔABC, then prove that :
8rR{cos2A/2+cos2B/2+cos2C/2}
=2bc+2ca+2ab−a2−b2−c2.
View SolutionIf r is the radius of the in circle of a right triangle prove that r=(a+c-b)/2 BP=BQ=r ,AP=AR=c-r,CR=CQ=b-r,b =c-r+a-r.
View Solution
