A thin wire carries a uniformly distributed charge Q = 3. 14nC along its length. The wire is bent in the form of a semi-circular arc of radius R = 1 m (without disturbing the charge distribution). Find the electric field at the center of curvature of the arc (in N/C).
The correct Answer is:0018
To find the electric field at the center of curvature of a semi-circular arc of radius R=1m carrying a uniformly distributed charge Q=3.14nC, we can follow these steps:
Step 1: Calculate the Linear Charge Density
The linear charge density λ is defined as the total charge per unit length. For a semi-circular arc, the length L of the arc is given by:
L=πR
Substituting R=1m:
L=π×1=πm
Now, we can find λ:
λ=QL=3.14×10−9Cπm=3.14×10−93.14=10−9C/m
Step 2: Use the Electric Field Formula for a Semi-Circular Arc
The electric field E at the center of a semi-circular arc due to a uniformly charged wire is given by the formula:
E=2kλR
where k is Coulomb's constant, approximately 9×109N m2/C2.
Step 3: Substitute the Values into the Formula
Substituting λ=10−9C/m and R=1m:
E=2×9×109N m2/C2×10−9C/m1m
This simplifies to:
E=2×9=18N/C
Step 4: Conclusion
The electric field at the center of curvature of the semi-circular arc is:
E=18N/C
The linear charge density λ is defined as the total charge per unit length. For a semi-circular arc, the length L of the arc is given by:
L=πR
Substituting R=1m:
L=π×1=πm
Now, we can find λ:
λ=QL=3.14×10−9Cπm=3.14×10−93.14=10−9C/m
The electric field E at the center of a semi-circular arc due to a uniformly charged wire is given by the formula:
E=2kλR
where k is Coulomb's constant, approximately 9×109N m2/C2.
Substituting λ=10−9C/m and R=1m:
E=2×9×109N m2/C2×10−9C/m1m
This simplifies to:
E=2×9=18N/C
The electric field at the center of curvature of the semi-circular arc is:
E=18N/C
Topper's Solved these Questions
Similar Questions
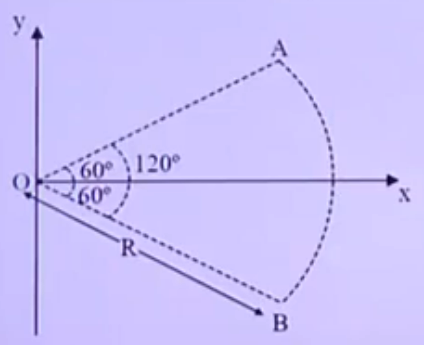
Figure shows a rod AB, which is bent in a 120∘ circular arc of radius R. A charge (-Q) is uniformly distributed over rod AB. What is the electric field →E at the centre of curvature O ?
View SolutionA wire of length l and charge q is bent in form of a semicircle. The charge is uniformly distributed over the length. The electric field at the centre of semicircle is
View Solution
Knowledge Check
A charged wire is bent in the form of a semicircular arc of radius a. If charge per unit length is λ coulomb/metre, the electric field at the centre O is
Aλ2πa2ε0Bλ4π2ε0aCλ2πε0aDzeroA thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is
 A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆj
A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆj(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
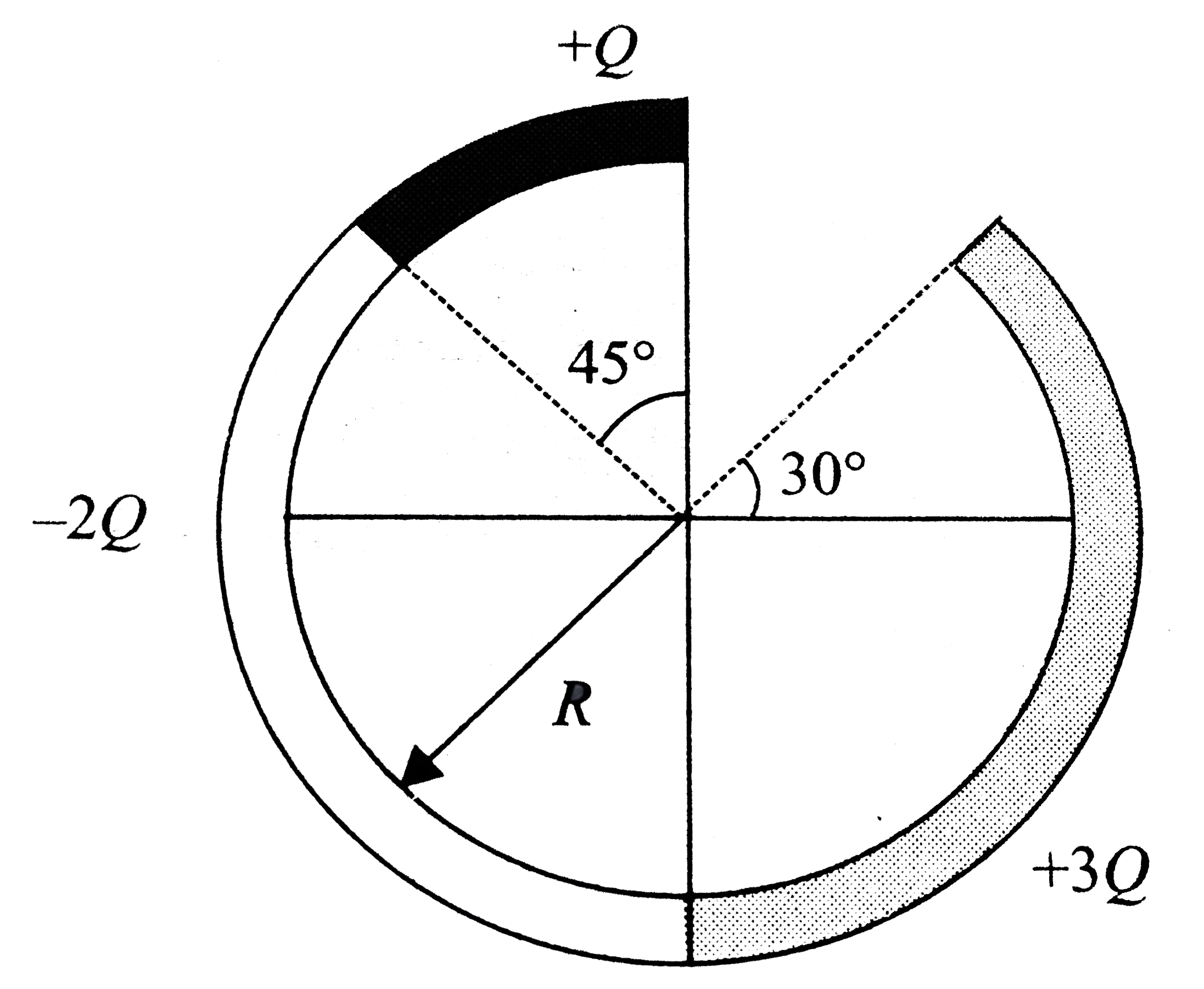 .Aq2πε0RB5Q12πε0RC3Q32πε0RDnone of these.
.Aq2πε0RB5Q12πε0RC3Q32πε0RDnone of these.
Find the electric field due to an uniformly charged arc, at the center 'c'.

View SolutionA rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
View SolutionA positive charge Q is uniformly distributed across a rod of length L. The rod is then bent in the form of a semicircle. What will be the electric field intensity at the centre of curvature of the semicircle thus formed?
View SolutionA thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is

View SolutionA wire is bent to form a semi circle such that the radius of the semicircle is R. The charge per unit length is λ. The total electric field at the centre will be
View Solution

