A particle A of mass m moving on a smooth horizontal surface collides with a stationary particle B of mass 2m directly, situated at a distance d from a wall. The coefficient of restitution between A and B and between B and the wall is e = 1/4. Calculate the distance from the wall where they collide again. Assume that the entire motion takes place along a straight line perpendicular to the wall.
The correct Answer is:[12d/13]
Step by step video, text & image solution for A particle A of mass m moving on a smooth horizontal surface collides with a stationary particle B of mass 2m directly, situated at a distance d from a wall. The coefficient of restitution between A and B and between B and the wall is e = 1/4. Calculate the distance from the wall where they collide again. Assume that the entire motion takes place along a straight line perpendicular to the wall. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In which o the following cases the centre of mass of a rod is certainly not at its centre?
View SolutionA ball is projected from the ground with speed u at an angle alpha with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA ball A of mass 3 m is placed at a distance d from the wall on a smooth horizontal surface Another ball B of mass m moving with velocity u collides with ball A . The coefficient of restitution between the balls and the wall and between the balls is e (a) the velocity of ball B after collision is (u(3e-1))/(4) . (b) the velocity of ball B after collision is (u(2e-1))/(4) . ( c) after collision, ball A will have away by distance (d(2e-1))/((2e-1)) during the time ball B returns back to wall. (d) after collision, ball A will move away by distance (d(e-1))/((3e-1)) during the time ball B returns back to wall.
View SolutionTwo particles A and B of masses 2m and m are placed on a smooth surface at separation d. They move towards each other due to the mutual attractive force.
(i) The particles will meet at distance d/3 from the initial position of mass 2m.
(ii) The speed of A will be half of speed of B until the particles collide (excluding the initial speed).
(iii) The distance covered by B is always double that covered by A until the particles collide.
(iv) The velocity of center of mass is always zero.
View SolutionA particle A of mass m is situated at highest point of wedge B of mass 2m is released from rest. Then distance travelled by wedge B( with respect to ground ) when particle A reaches at lowest position. Assume all surfaces are smooth.

View SolutionA particle moving on a smooth horizontal surface strikes a stationary wall. The angle of strike is equal to the angle of rebound & is equal to 37∘ and the coefficient of restitution with wall is e=15. Find the friction coefficient between wall and the particle form X10 and fill value of X :
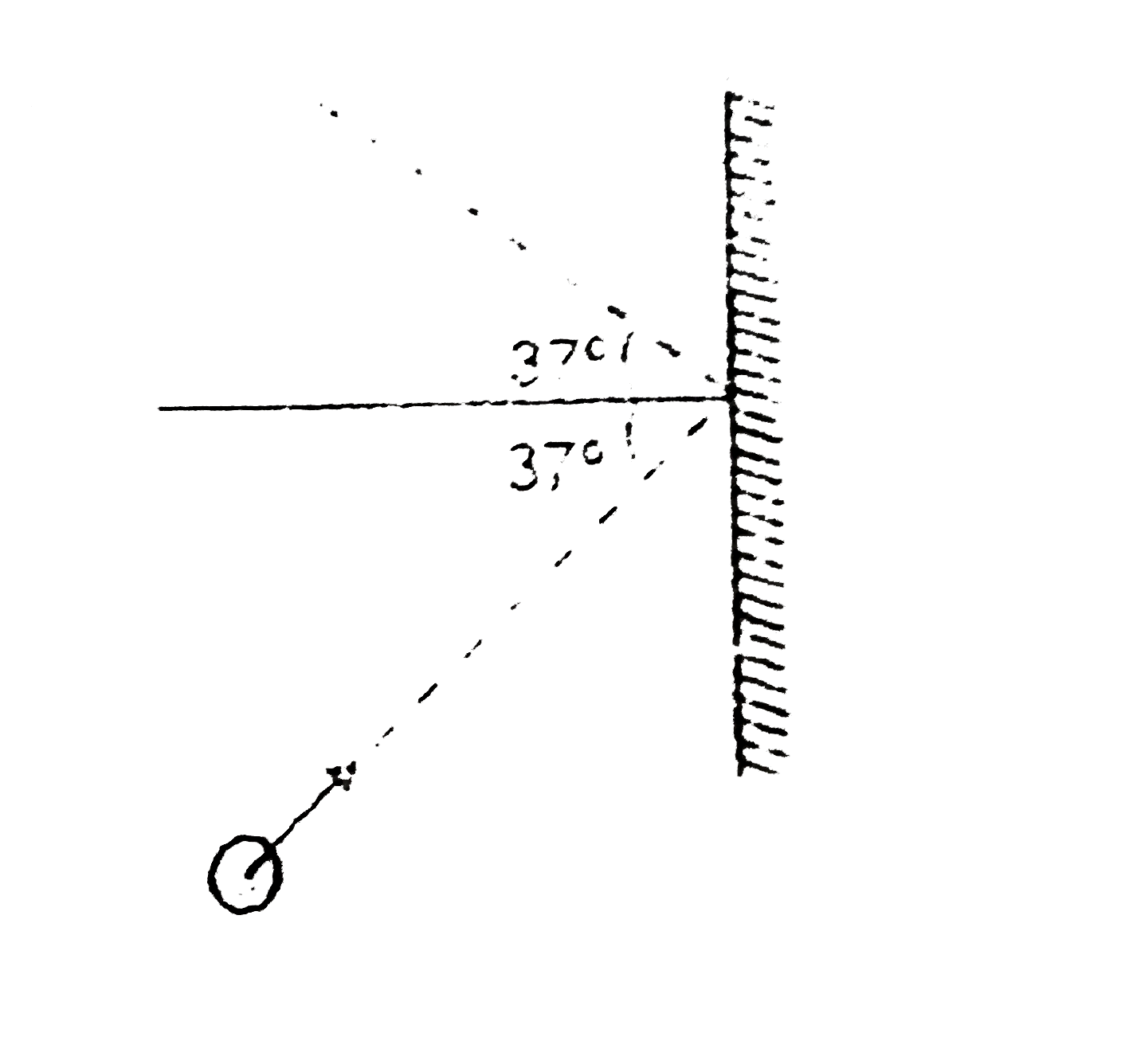
View SolutionA particle of mass m_(1) collides head on with a stationary particles of mass m_(2) . If (m_(1))/(m_(2)) gte, where e is the coefficient of restitution, then :
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m//s and 2m//s respectively collides each other. Coefficient of restitution is e=(1)/(2) , then Velocity of A after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Velocity of B after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Loss in kinetic energy in collision
View SolutionA smooth sphere of mass m is moving on a horizontal plane with a velocity (3ˆi+ˆj) . It collides with smooth a vertical wall which is parallel to the vector ˆj . If coefficient of restitution e=12 then impulse that acts on the sphere is
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance .a. from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA ball is projected from the ground with speed u at an angle alpha with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
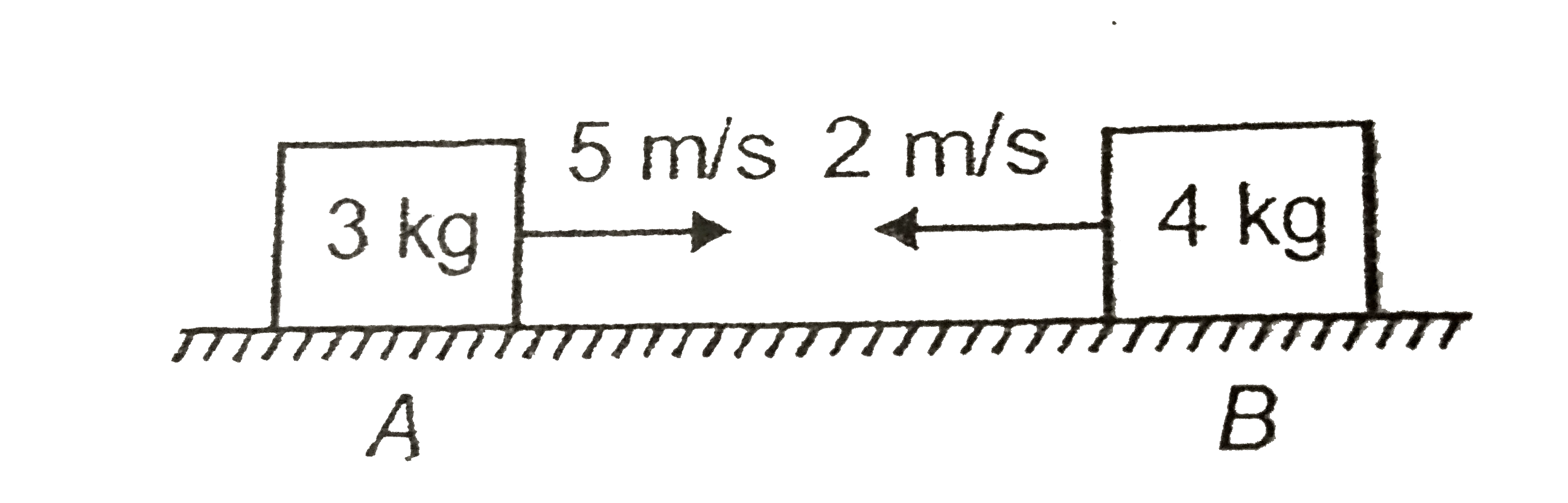
Velocity of A after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m//s and 2m//s respectively collides each other. Coefficient of restitution is e=(1)/(2) , then Velocity of B after collision
View Solution
