ABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that CQ=13BC. Prove that AQCP is a parallelogram.
To prove that quadrilateral AQCP is a parallelogram, we will follow these steps:
Step 1: Understand the Given Information
We have a parallelogram ABCD where:
- P is a point on AD such that AP=13AD
- Q is a point on BC such that CQ=13BC
Step 2: Use Properties of Parallelograms
Since ABCD is a parallelogram, we know:
- AD∥BC
- AD=BC
Step 3: Relate the Segments
From the information given:
- Since AP=13AD, it follows that PD=AD−AP=AD−13AD=23AD.
- Similarly, since CQ=13BC, we have BQ=BC−CQ=BC−13BC=23BC.
Step 4: Establish Parallelism
Since AD∥BC, we can conclude that:
- AP∥CQ because both segments are parts of lines that are parallel to each other.
Step 5: Establish Equality of Lengths
From the previous steps, we have:
- AP=13AD and CQ=13BC
- Since AD=BC (as sides of the parallelogram), we can say AP=CQ.
Step 6: Conclude that AQCP is a Parallelogram
Now we have:
- AP∥CQ (both are parallel)
- AP=CQ (both are equal)
By the definition of a parallelogram, if one pair of opposite sides are both equal and parallel, then the quadrilateral AQCP is a parallelogram.
Final Conclusion
Thus, we have proved that AQCP is a parallelogram.
---
We have a parallelogram ABCD where:
- P is a point on AD such that AP=13AD
- Q is a point on BC such that CQ=13BC
Since ABCD is a parallelogram, we know:
- AD∥BC
- AD=BC
From the information given:
- Since AP=13AD, it follows that PD=AD−AP=AD−13AD=23AD.
- Similarly, since CQ=13BC, we have BQ=BC−CQ=BC−13BC=23BC.
Since AD∥BC, we can conclude that:
- AP∥CQ because both segments are parts of lines that are parallel to each other.
From the previous steps, we have:
- AP=13AD and CQ=13BC
- Since AD=BC (as sides of the parallelogram), we can say AP=CQ.
Now we have:
- AP∥CQ (both are parallel)
- AP=CQ (both are equal)
Thus, we have proved that AQCP is a parallelogram.
Topper's Solved these Questions
Similar Questions
1000 families with 2 children were selected randomly and the following data were recorded.
∣∣∣Number of boys in a family 0 1 2Number of families 140 560 300∣∣∣
If a family is chosen at random, find the probability that it has
(i) no boy
(ii) one boy
(iii) two boys
(iv) at least one boy
(v) at most one boy.
View SolutionIf x=3+√8 , find the value of x2+1x2
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔABC
(iv) AQ=CP
(v) APCQ is a parallelogram.

View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
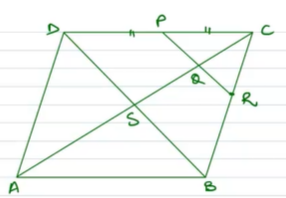
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn A ABC , P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar(PRQ)=12ar(ARC)
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔAQB≅ΔCPD
(iv) AQ=CP
(v) APCQ is a parallelogram.

View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR ABCD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View Solution
