चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर बिंदु P पर प्रतिच्छेद करते है । प्रदर्शित कीजिए कि
ar(ΔAPB)×ar(ΔCPD)=ar(ΔAPD)×ar(ΔBPC)
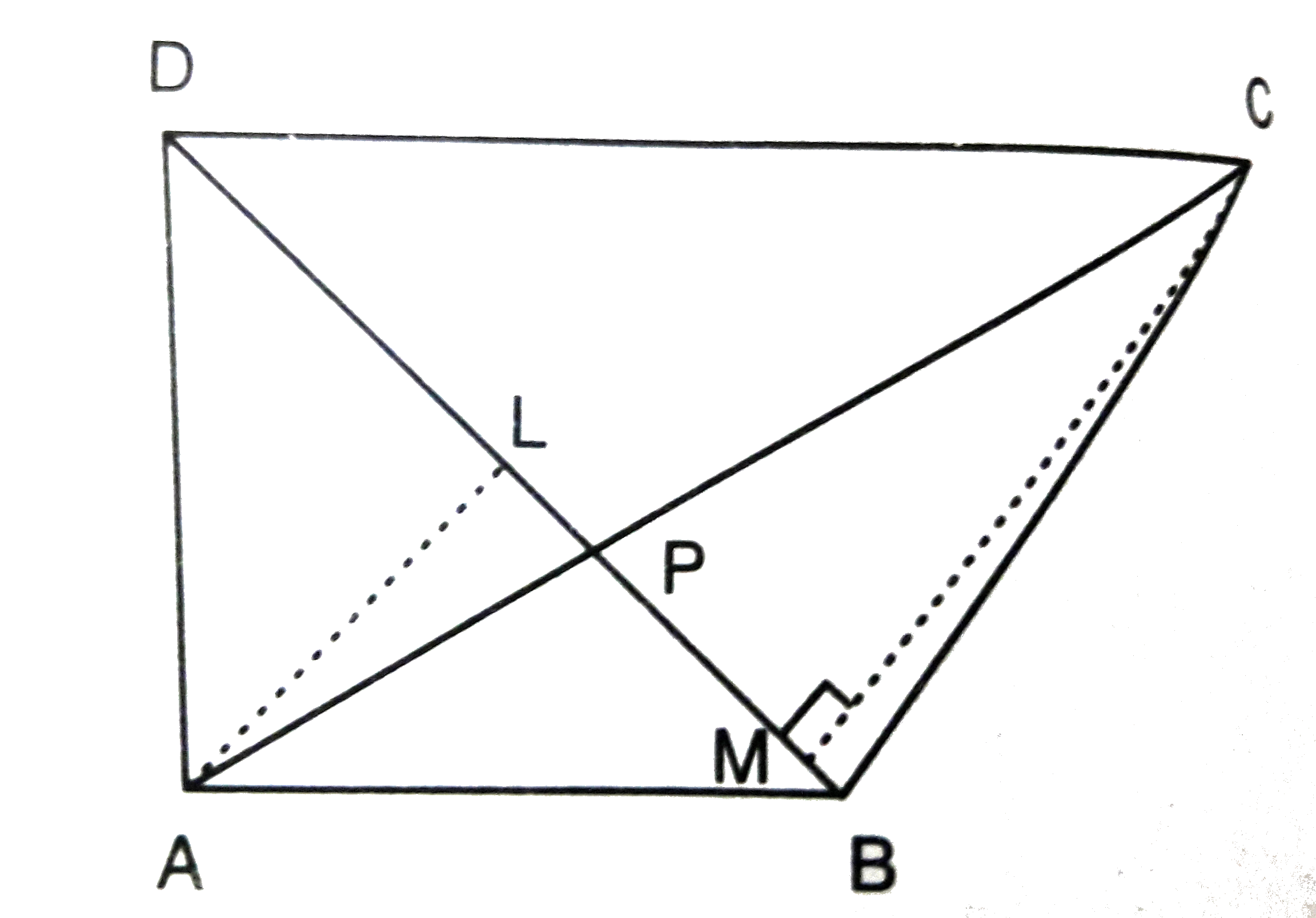
ar(ΔAPD)×ar(ΔBPC)
={12×AL×DP}×{12×CM×BP}
={12(BP×AL)}×{12(DP×CM)}
=ar(ΔAPB)×ar(ΔCPD)
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
निम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of square ABCD intersect each other at point P. Show that ar(/_APB)xx ar(/_CPD)=ar(/_APD)xx ar(/_BPC)
View SolutionIn the adjoining figure, P is the point in the interior of a parallelogram ABCD.Show that ar(DeltaAPB) ar(DeltaPCD) =1/2ar(||gm ABCD)
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि
ar(APB)×ar(CPD)=ar(APD)×ar(BPC)
View Solutionएक चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर इस प्रकार प्रतिच्छेद करते हैं कि ar(ΔAOD)=ar(ΔBOC) है । सिद्ध करों कि ABCD एक समलम्ब है।
View Solutionएक चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि ar(AOD) = ar(BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब है।
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर चतुर्भुज के भीतर काटते है तो
ar(ABCD)=ar(ABC)+ar(…….).
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPD).
[Hint : From A and C, draw perpendiculars to BD.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC) . Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD each other at P. Show that ar (APB) × ar (CPD) =ar (APD) × ar (BPC)
View SolutionP is a point in the interior of a parallelogram ABCD. Show that
(i) ar (ΔAPB)+ar(ΔPCD)=12ar(ABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)
(Hint : Throught , P draw a line parallel to AB)
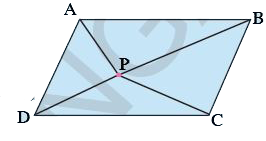
View SolutionP is a point in the interior of a parallelogram ABCD. Show that
(i) ar (ΔAPB)+ar(ΔPCD)=12ar(ABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)
(Hint : Throught , P draw a line parallel to AB)
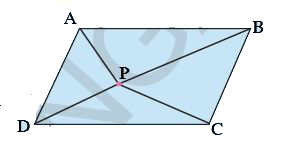
View SolutionP is a point in the interior of a parallelogram ABCD. Show that
(i) ar (ΔAPB)+ar(ΔPCD)=12ar(ABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)
(Hint : Throught , P draw a line parallel to AB)
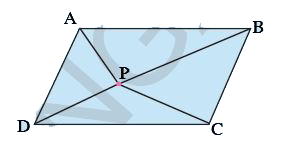
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of quadrilateral ABCD intersect each other at P. Show that ar (APB)×ar(CPD) = ar (APD)×ar(BPC).
View Solution