ABCD एक समांतर चतुर्भुज है जिसमें BC को E तक इस प्रकार आगे बढ़ाया गया है कि CE = BC तथा रेखाखण्ड AE रेखा CD को F पर प्रतिच्छेद करती है , तो
(i )सिद्ध कीजिए कि ar(ΔADF)=ar(ΔECF)
(ii) यदि ΔDFB का क्षेत्रफल = 3 सेमी2, तो ।।gm ABCD का क्षेत्रफल ज्ञात कीजिए।
The correct Answer is:(ii) 12 सेमी2
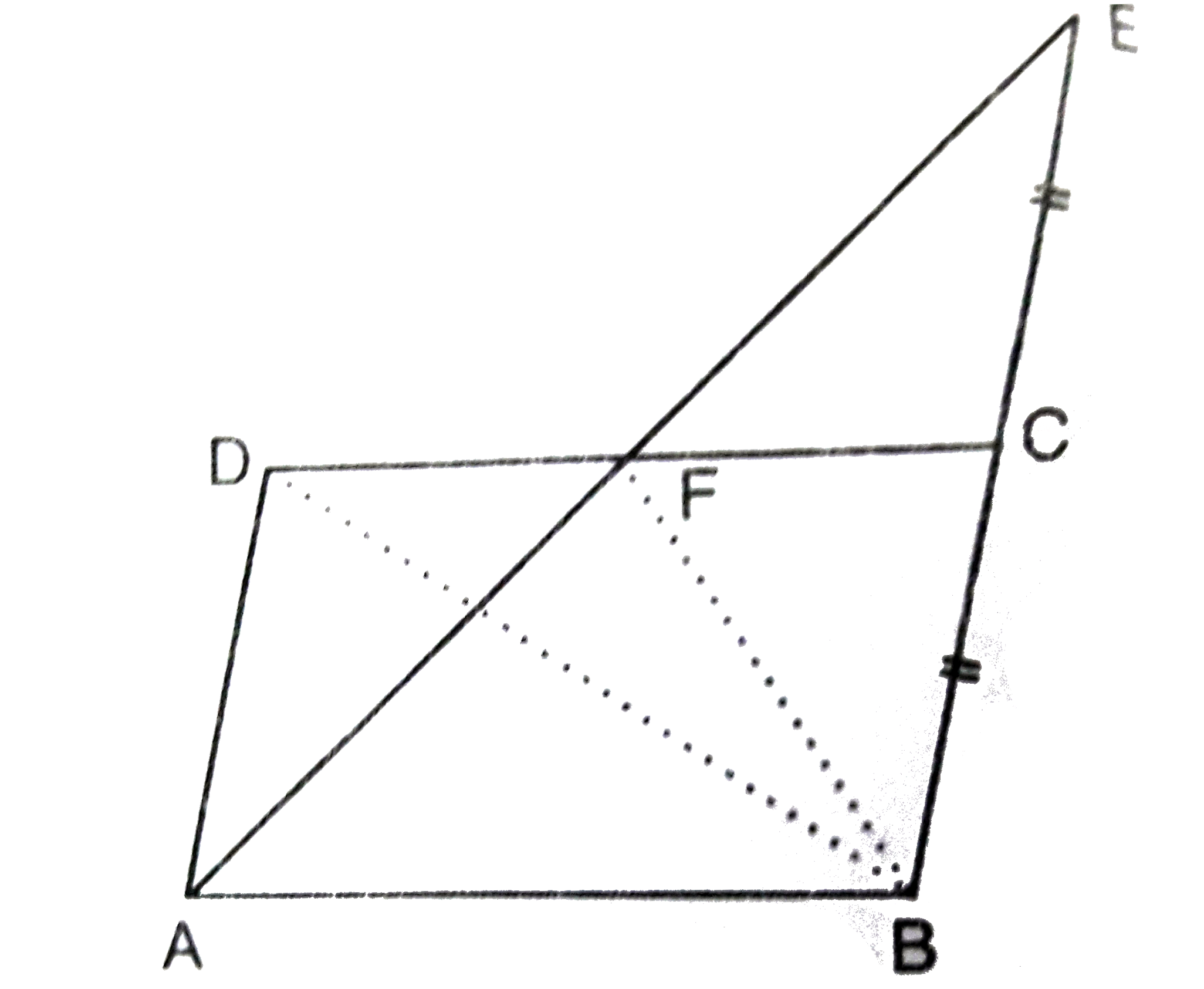
त्रिभुज ADF तथा ECF में,
∠ADF=∠ECF
AD=EC
तथा ∠DFA=∠CFA
अतः कोण- कोण-भुजा सर्वांगसमता अभिगृहित से
ΔADF≅ΔECF
⇒ar(ΔADF)=ar(ΔECF) और DF=CF
चूँकि DF=CF
⇒BF,ΔBCD की एक माध्यिका है।
⇒ar(ΔBCD)=2ar(ΔBDF)
⇒ar(ΔBCD)=2×3सेमी2=6सेमी2
अतः ar( समांतर □ABCD)=2ar(ΔBCD)=2×6=12 वर्ग सेमी
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
निम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionरेखा 4x+3y=12 अक्षो को बिन्दुओ L और M पर प्रतिच्छेद करती है बिंदु इस प्रकार गति करता है की त्रिभुज PLM का क्षेत्रफल सदैव वर्ग इकाई रहता है , तो P का बिन्दुपथ ज्ञात कीजिये
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionयदि बिंदुओं A और B के स्थिति सदिश क्रमशः ¯a और ¯b हों तो उस बिंदु C का स्थिति सदिश ज्ञात कीजिए जो BA को आगे बढ़ने पर इस प्रकार स्थित है कि BC=1.5BA.
View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि y2+2ax+2by+c=0 एक परवलय को निरूपित करता है जिसका अक्ष x-अक्ष के समांतर है। इसका शीर्ष तथा इसके नाभिलम्ब का समीकरण ज्ञात कीजिए।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionएक समतल निर्देशाक्षों को क्रमश: A, B तथा C पर काटता है। यदि △ABC का केन्द्रक (2,-1, 3) है, तो समतल का समीकरण ज्ञात कीजिए।
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View SolutionABCD is a parallelogram in which BC is produced to E such that CE=BC and AE intersects CD at F.
If ar.(ΔDFB)=30cm2, find the area of parallelogram
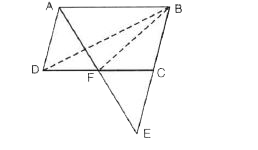
View SolutionPQRS is a parallelogram and its area is 300 cm2. Side PQ is extended to X such that PQ=QX. If XS intersects QR at Y, then what is the area (in cm2) of triangle SYR?
PQRS एक समांतर चतुर्भुज है तथा 300 से.मी.2 है। भुजा को तक इस तरह बढाया गया कि PQ=QX है। यदि XS, QR को Y पर काटता है, तो त्रिसुज SYR का क्षेत्रफल (से.मी.2 में) क्या हैं?
View Solution
