चित्र में, ABCD तथा AEFD दो समांतर चतुर्भुज है। सिद्ध कीजिए कि :
(i) PE=FQ
( ii) ar(ΔAPE):ar(ΔPEA)=ar(ΔQFD):ar(ΔPFD)
(iii) ar(ΔPEA)=ar(ΔQFD)
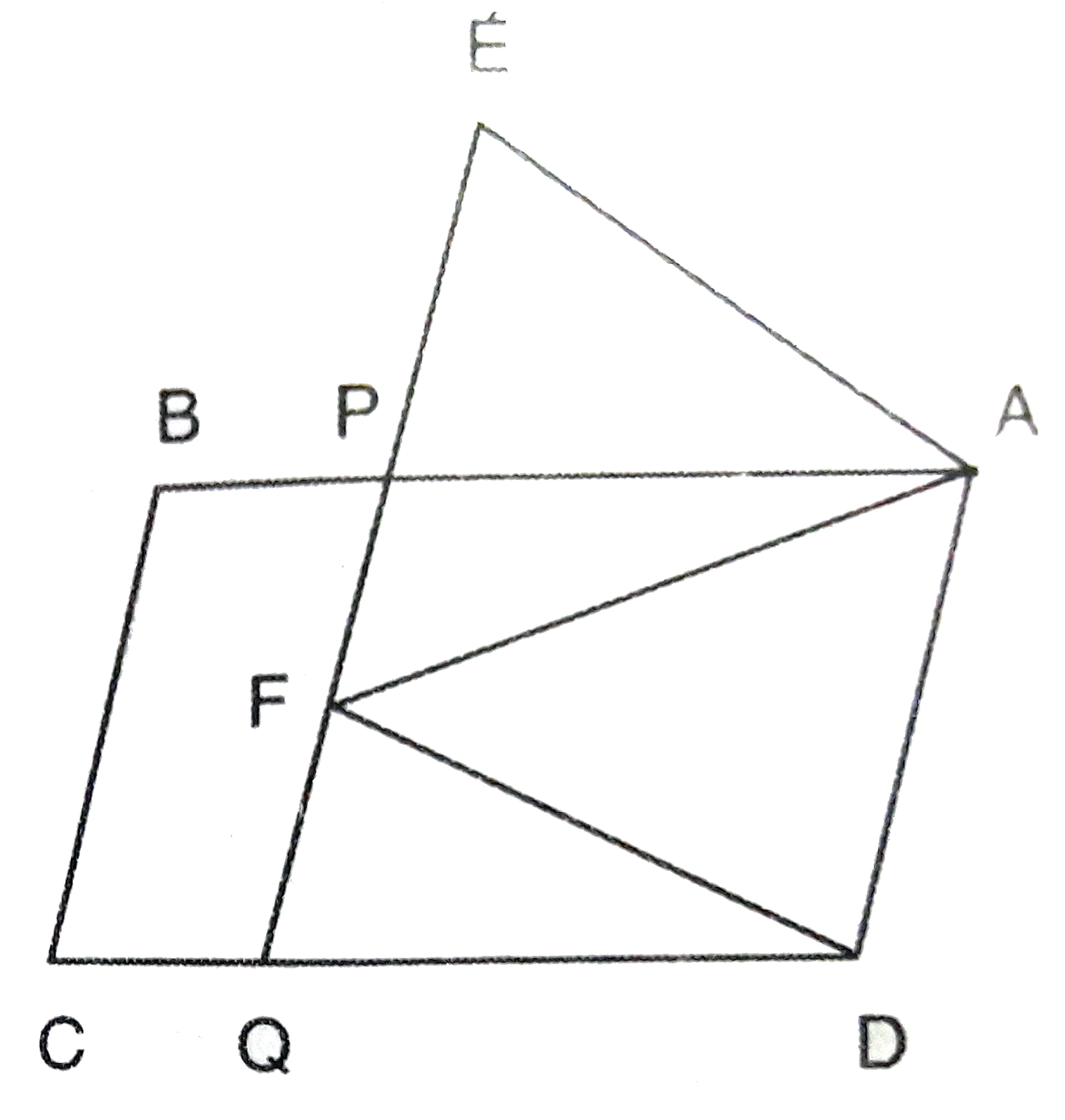
(i) त्रिभुज APE तथा त्रिभुज DQF पर विचार करते है। इन दोनों त्रिभुजों में
∠APE=∠DQF
AE=DF
∠AEP=∠DFQ
अतः कोण-कोण-भुजा सर्वांगसम अभिगृहित से,
ΔAPE≅ΔDQF
⇒PE=QF तथा ar(ΔAPE)=ar(ΔDQF) ...(i)
इस प्रकार (i ) और (iii ) सत्यापित हो जाते है।
(ii ) स्पष्ट है कि त्रिभुज PFA तथा त्रिभुज PFD एक ही आधार PF पर और एक ही समांतर रेखाओं PQ और AD के बीच स्थित है।
∴ar(ΔPFA)=ar(ΔPFD) ...(ii)
(i ) तथा (ii ) से ,
ar(ΔAPE)ar(ΔPFA)=ar(ΔDQF)ar(ΔPFD)
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
निम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
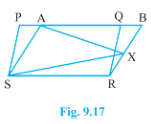
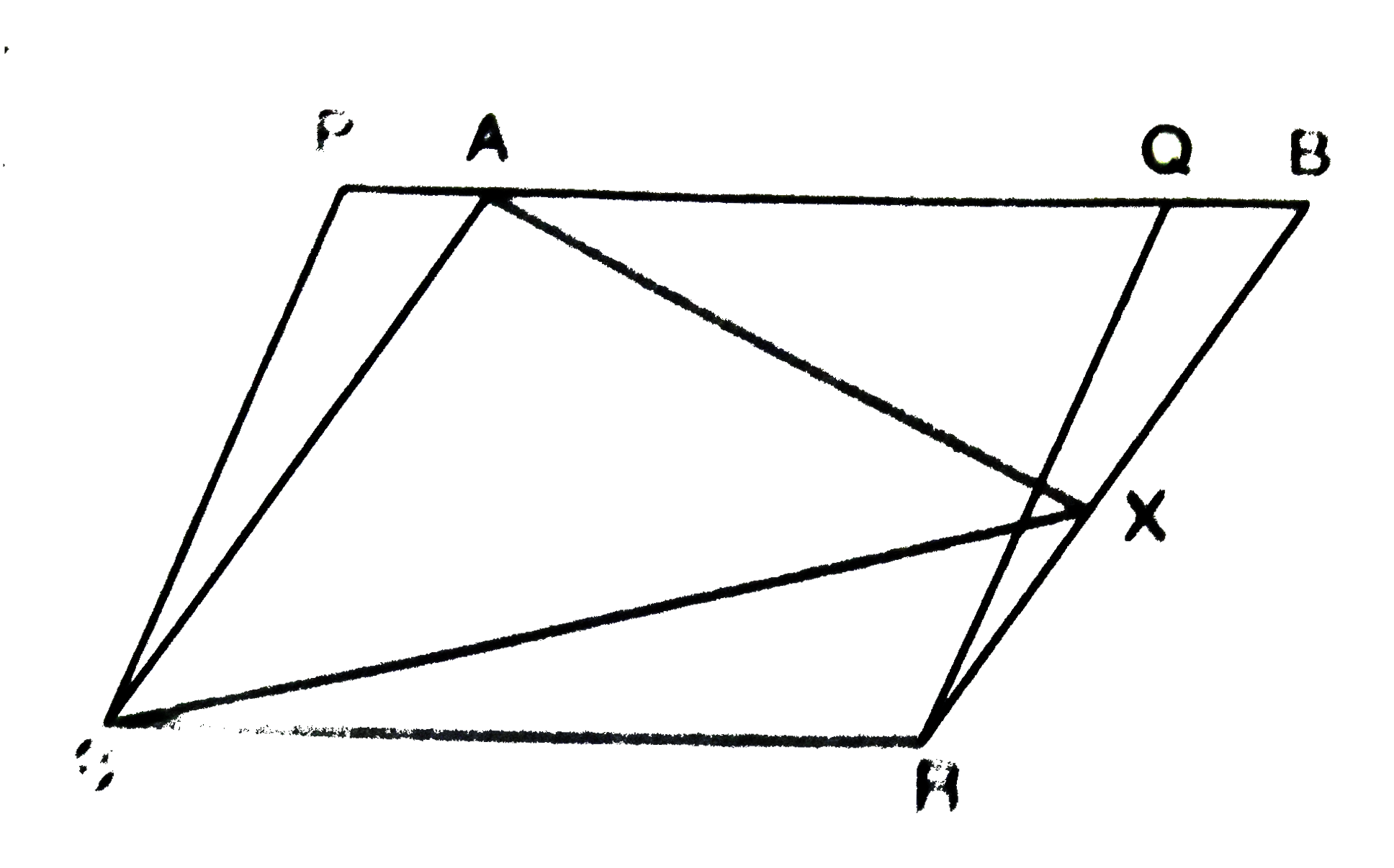
View SolutionIn Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar(PQRS)=ar(ABRS)(ii) ar(AXS) =12ar(PQRS)
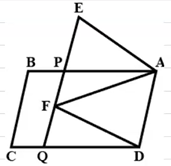
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View Solutionआकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(APB)+ar(PCD)=12ar(ABCD)
(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View Solutionआकृति में, PQRS और ABRS समांतर चतुर्भुज है तथा X भुजा BR स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(PQRS)=ar(ABRS)
(ii) ar(AXS)=12ar(PQRS)
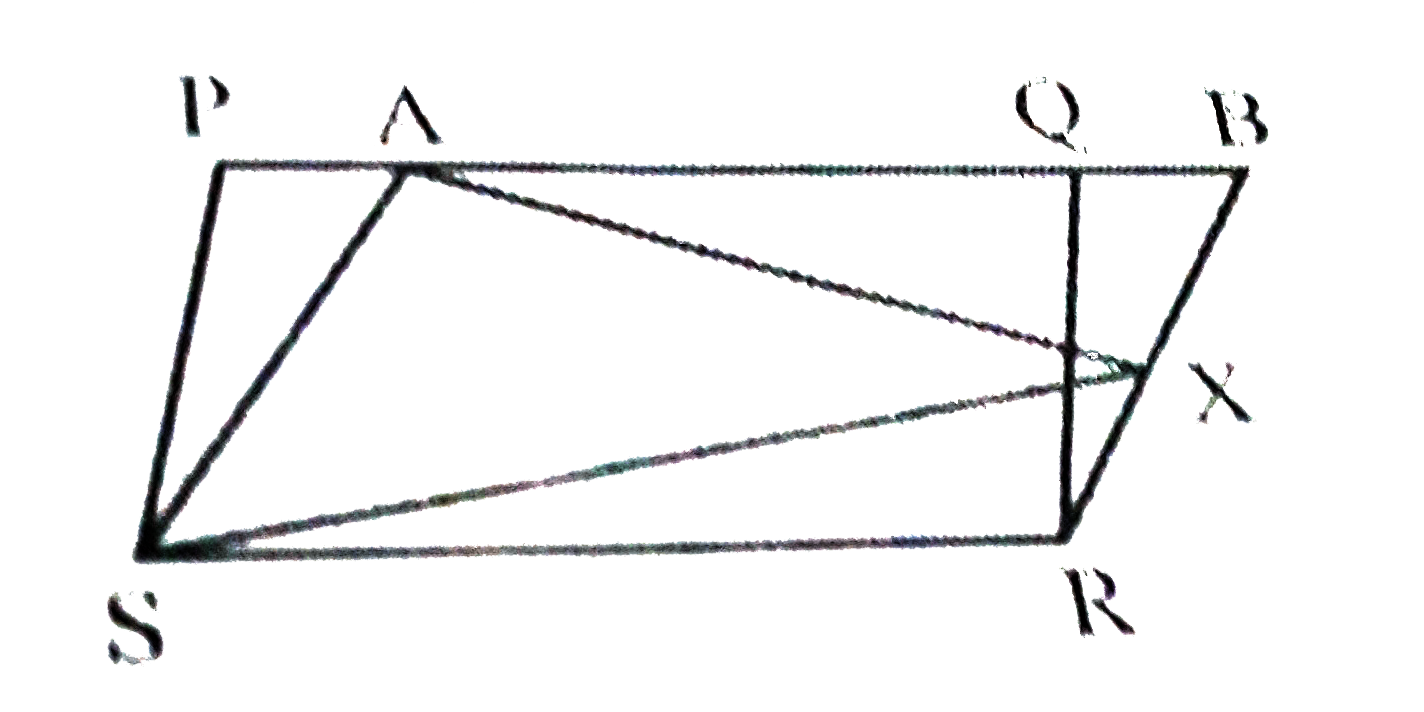
View Solutionचित्र में PQRS तथा ABRS समान्तर चतुर्भुज है तथा X भुजा BR पर स्थित कोई बिंदु है। दर्शाए कि
(i)ar(||gmPQRS)=ar(||gmABRS) (ii)ar(ΔAXS)=12ar(||gmPQRS)
View SolutionABCD एक समांतर चतुर्भुज है तथा O इसके अन्तः क्षेत्र में स्थित कोई बिंदु है सिद्ध कीजिए कि
(i) ar(ΔAOB)+ar(ΔCOD)=ar(ΔBOC)+ar(ΔAOD)
(ii) ar(ΔAOB)+ar(ΔCOD)=12ar(।।gmABCD)
View SolutionF,Cl, Br ,I and Ar are collectively known as ____________.
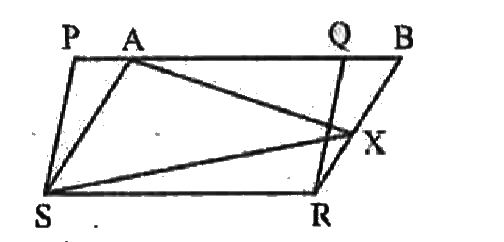
View SolutionIn, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar (PQRS) = ar (ABRS)
as (AXS) = 12 ar (PQRS)
View SolutionFactorise:
ar+br+at+bt
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View SolutionIn the Fig Prove that XA+AR=XB+BR.
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View Solution