A semicircular wire of radius R is oriented vertically. A small bead is released from rest from the top of the wire. It slides without friction under the influence of gravity to the bottom, where it then leaves the wire horizontally and falls distance H to the ground. The bead lands a horizontal distance D away from where it was launched. Which of the following is correct graph of RH vetsus D2?
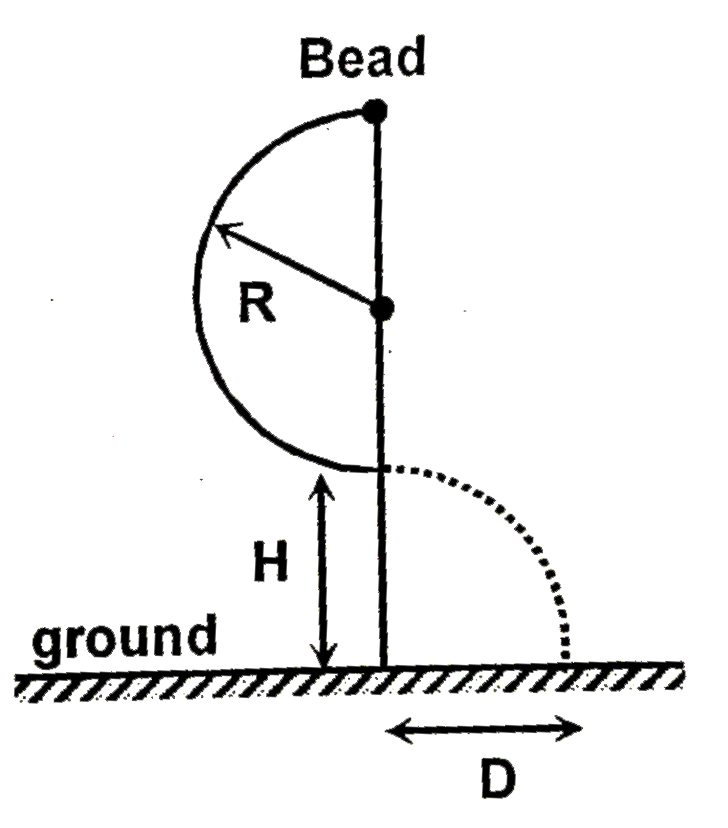
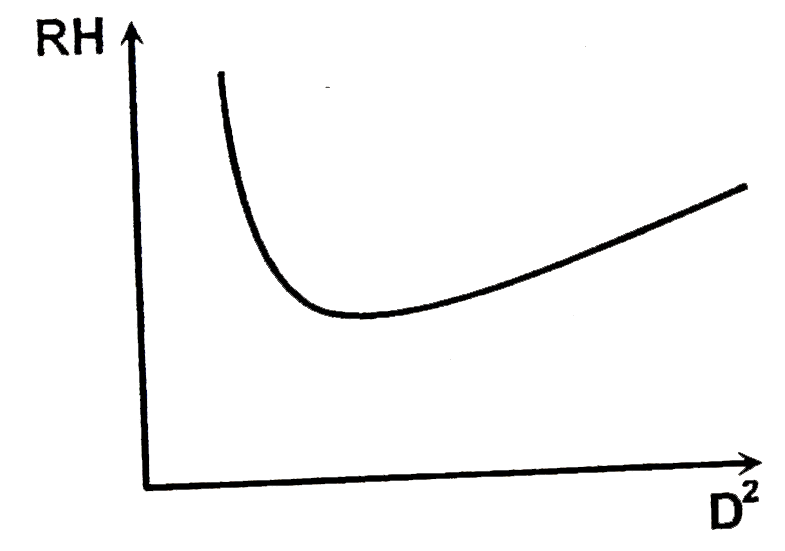
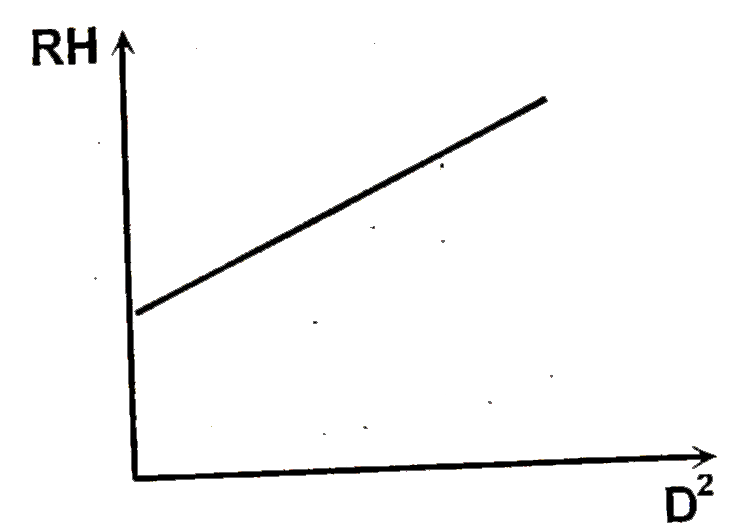
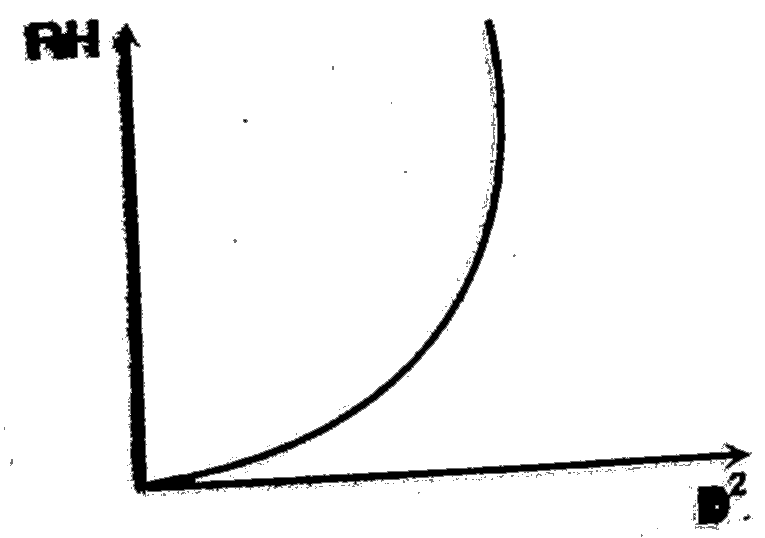
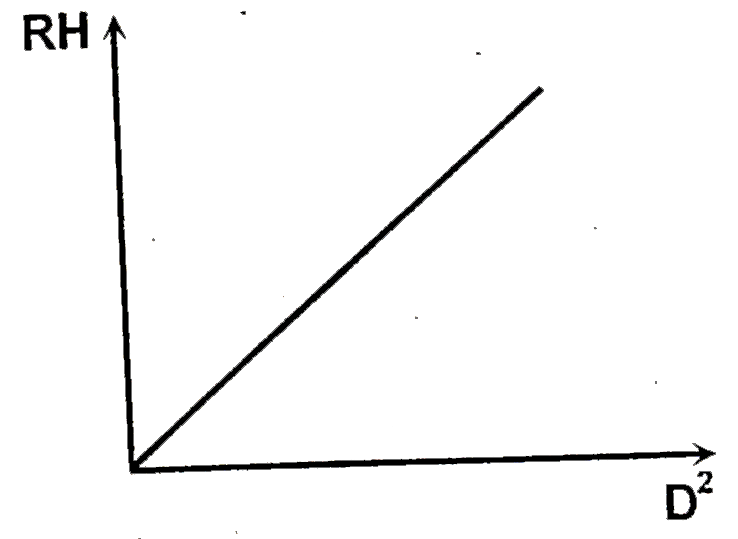
The correct Answer is:D
D=√2Hg√2g(2R)
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions

A particle of mass 3m is projected from point-A with speed 3v0 as shown in figure. When the particle is at point P, it explodes in three identical particles choose the INCORRECT statement regarding the physical quantities just before and just after explosion
View SolutionA particle moves in x-y plane according to the equation ¯r=(ˆi+2ˆj)Acosωt. The motion of the particle is
View SolutionThe potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=ax12−bx4, where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The graph between potential energy vs x will be
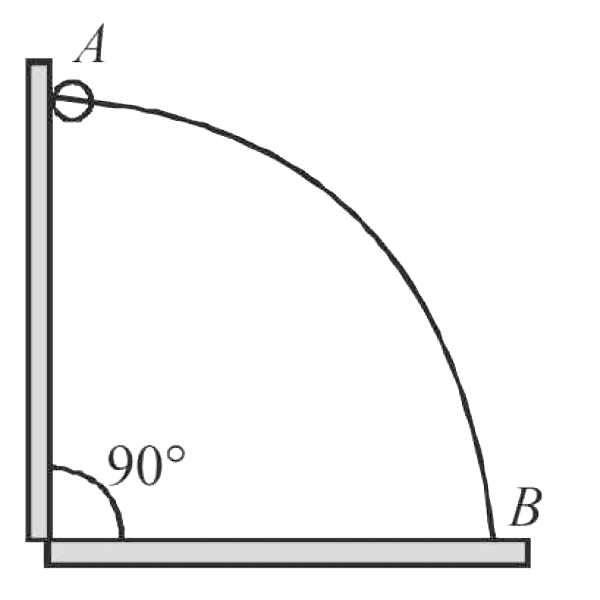
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View SolutionA piece of wire is bent in the shape of a parabola y = Kx^(2) (y - axis vorical) with a bead of mass m on it . The beat can side on the wire without friction , it stays the wire is now accleated parallel to the bead , where the bead can stay at rest with repect to the wire from the y - axis is
View SolutionA semicircular wire frame of radius R is standing vertical on a horizontal table. It is pulled horizontally towards right with a constant acceleration. A bead of mass m remain in equilibrium (relative to the semicircular wire) at a position where radius makes an angle q with horizontal. There is no friction between the wire and the bead. The bead is displaced a little bit in upward direction and released. Calculate the speed of the bead relative to the wire at the instant it strikes the table. Assume that all throughout the semicircular wire keeps moving with constant acceleration.
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass 'm' on it. The bead can slide on the wire without friction. The wire is now accelerated parallel to the x-axis where the with an acceleration'a'. The distance of the new equilibrium position of the bead is axgk where the bead can stay at rest with respect to the wire from y-axis. The value of x' is
View SolutionA piece of wire is bent in the shape of a parabola y = kx^2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View Solutionएक तार जो एक छोटे मोती के मध्य में स्थित छिद्र से गुजरता है, को एक चतुर्थाशा वृत्त के अनुरूप मोड़ा गया है। तार को भूमि पर उर्ध्व तल में स्थित किया गया है, जैसा चित्र में दर्शाया गया है । मोती को तार के ऊपरी सिरे से छोड़ा जाता है, जिससे यह तार के अनुदिश, बिना किसी घर्षण के सरकता है। जब मोती A से B तक सरकता है। तब इसके द्वारा तार पर लगने वाला बल है:
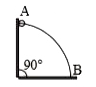
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx^(2) (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View Solution

