The graph pressure versus temperature (T) at constant volume is a straight line.(T/F)
The correct Answer is:A
To determine whether the statement "The graph of pressure versus temperature at constant volume is a straight line" is true or false, we can follow these steps:
Step 1: Understand the Ideal Gas Law
The Ideal Gas Law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
Step 2: Analyze the Condition of Constant Volume
In this scenario, we are considering a situation where the volume V is held constant. This means that any changes in pressure P will be directly related to changes in temperature T.
Step 3: Rearranging the Ideal Gas Law
Since volume is constant, we can rearrange the Ideal Gas Law to express pressure in terms of temperature:
P=nRVT
Here, nRV is a constant (let's call it k):
P=kT
Step 4: Interpret the Relationship
The equation P=kT shows that pressure P is directly proportional to temperature T when volume is constant. This indicates a linear relationship between pressure and temperature.
Step 5: Graphical Representation
If we plot pressure P on the y-axis and temperature T on the x-axis, the graph will be a straight line passing through the origin, with a slope equal to the constant k.
Conclusion
Since we have established that pressure is directly proportional to temperature at constant volume, the statement "The graph of pressure versus temperature at constant volume is a straight line" is True.
The Ideal Gas Law is given by the equation:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of gas
- R = universal gas constant
- T = temperature
In this scenario, we are considering a situation where the volume V is held constant. This means that any changes in pressure P will be directly related to changes in temperature T.
Since volume is constant, we can rearrange the Ideal Gas Law to express pressure in terms of temperature:
P=nRVT
Here, nRV is a constant (let's call it k):
P=kT
The equation P=kT shows that pressure P is directly proportional to temperature T when volume is constant. This indicates a linear relationship between pressure and temperature.
If we plot pressure P on the y-axis and temperature T on the x-axis, the graph will be a straight line passing through the origin, with a slope equal to the constant k.
Since we have established that pressure is directly proportional to temperature at constant volume, the statement "The graph of pressure versus temperature at constant volume is a straight line" is True.
Topper's Solved these Questions
Similar Questions
A plot of volume (V) versus temperature (T) for a gas at constant pressure is a straight line passing through the origin. The plots at different values of pressure are shown in figure. Which of the following order of pressure is correct for this gas ?

View SolutionA plot of volume (V) versus temperature (T) for a gas at constant pressure is a straight line passing through the origin . The plots at different values of pressure are shown in figure .
Which of the following order of pressure is correct for this gas ?

View Solution
Knowledge Check
Assertion:A constant volume gas thermometer, reads temperature in terms of pressure.
Reason : In this case a plot of Pressure versus temperature gives a straight line.AIf both assetion and reason are true and reaasons is the correct expanation of assetionBIf both assetion and reason are tur but reason is not the correct explanation of assetionCIf assertion is true but reason is falseDIf both assertion and reason are false.
A plot of volume (V) versus temperature (T) for a gas at constannt pressure is a straight line passing through the origin. The plots at different values of pressure are shown in figure. Which of the following order of pressure is correct for this gas?

View SolutionPressure versus temperature graph of an ideal gas at constant volume V is shown by the straight line A. Now mass of the gas is doubled and the volume is halved, then the corresponding pressure versus temperature graph will be shown by the line
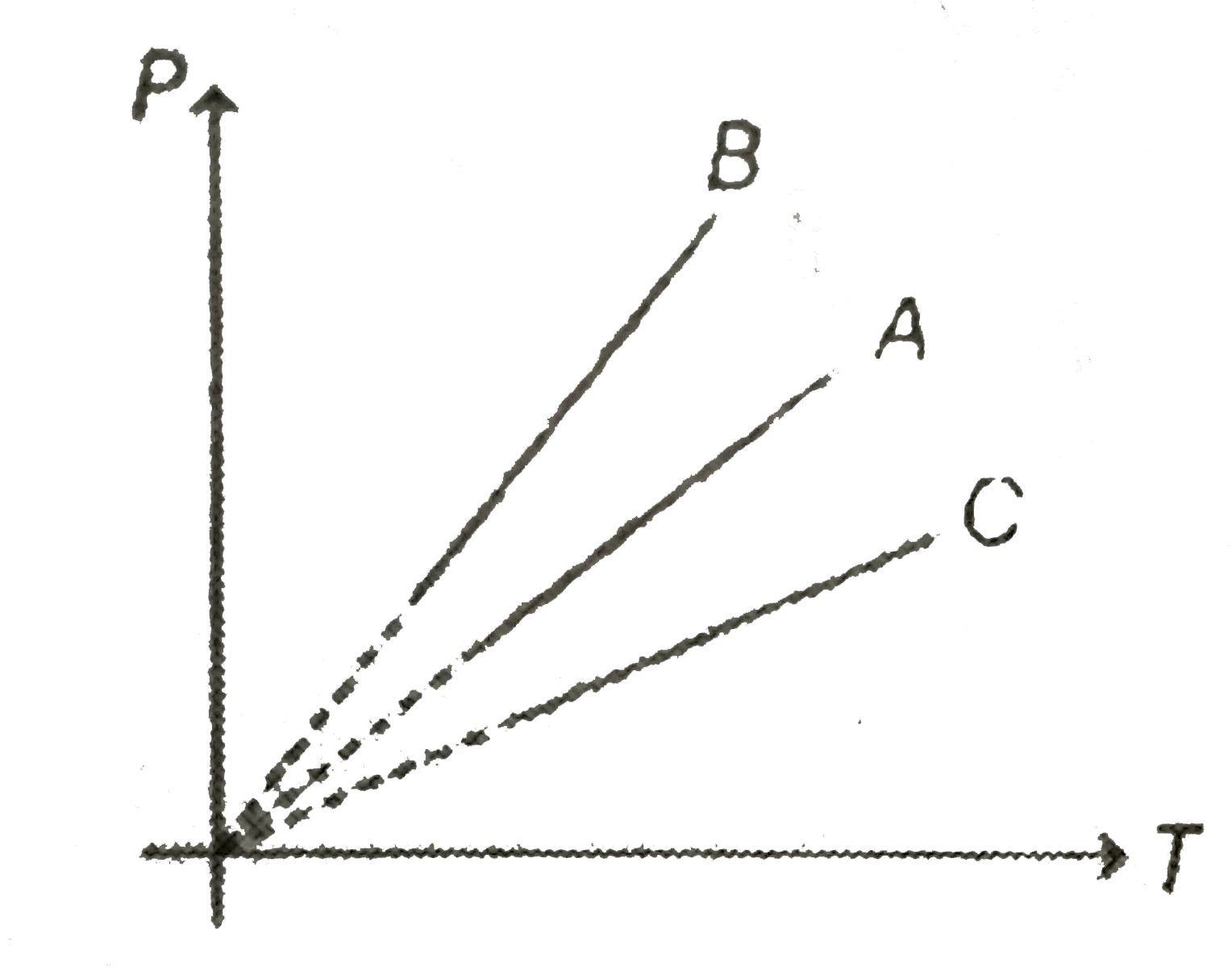
View SolutionIf we plot volume of a certain mass of a gas against temperature at constant pressure, we get a straight line intersecting on the negative side at −273.∘C which explains about absolute zero . This graph is known as
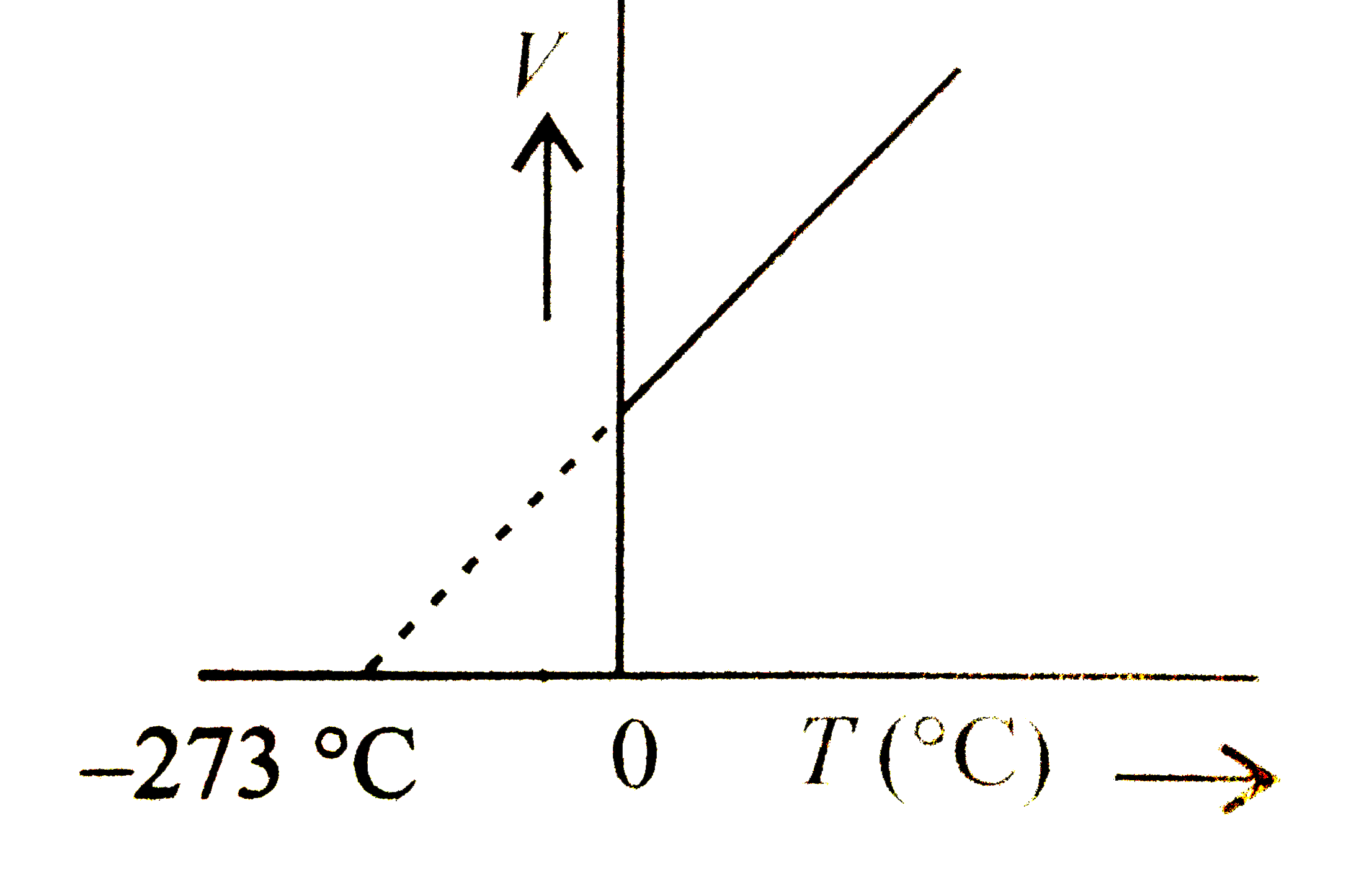
View SolutionThe graph between (P/T) and T for a gas at constant volume will be:
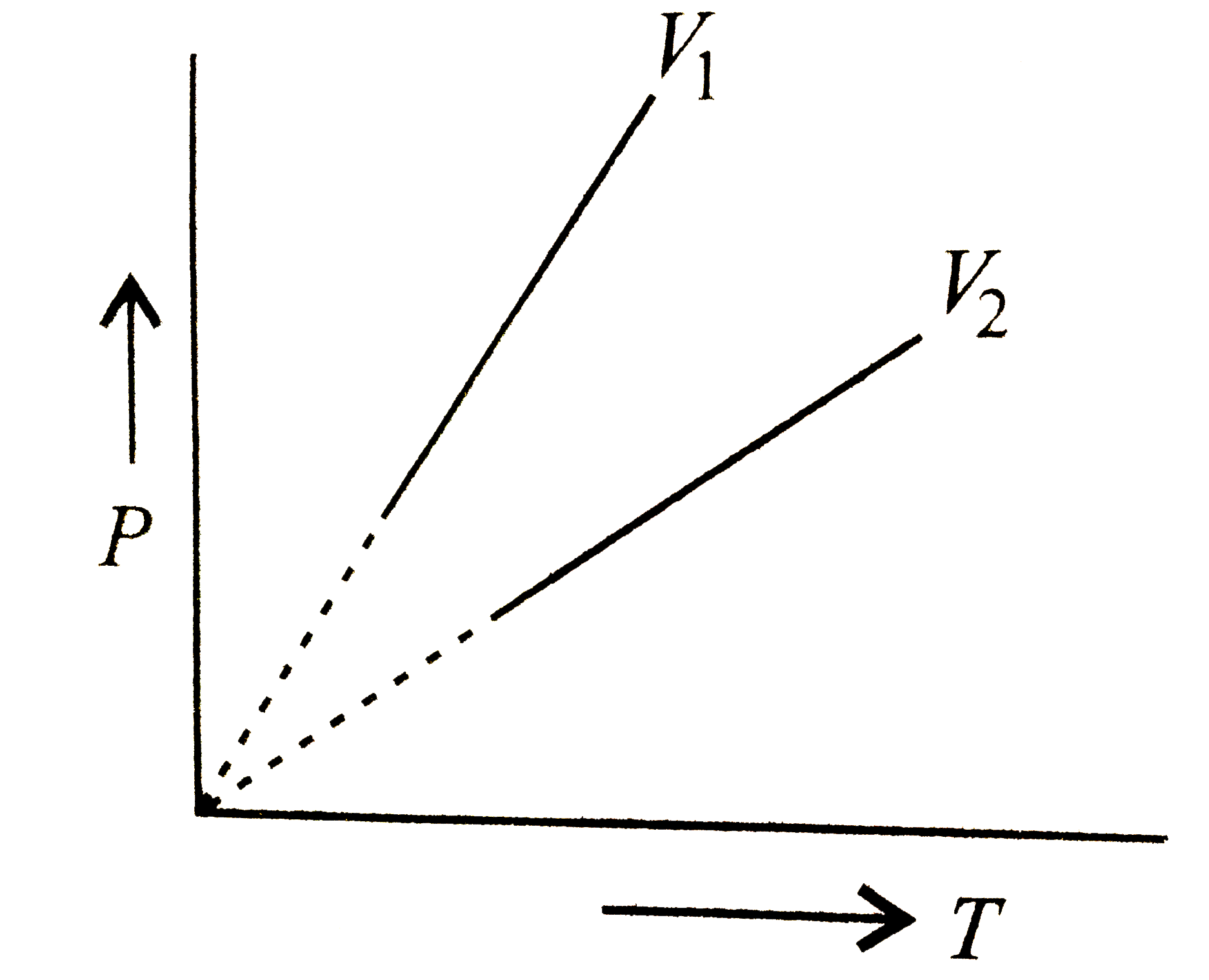
View SolutionA plot of P vs T for a given mass of gas at constant volume is a straight line . P vs T at constant volumes V1 and V2 for an ideal gas are shown below :
Which of the following is correct ?
View SolutionAssertion: The plot of volume (V) versus pressure (P) at constant temperature is a hyperbola in the first quadrant.
Reason: V∝1/P at constant temperature.
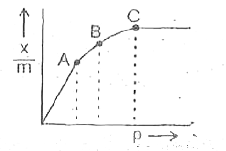
View SolutionThe graph plotted against adsorption versus pressure P at constant temperature, the Freundich equation at A, B, C respectively are (if n > 1)
View Solution

